Một mảnh đất hình chữ nhật ABCD có chiều dài \(AB = 25\;{\rm{m}}\), chiều rộng \(AD = 20\;{\rm{m}}\) được chia thành hai phần bằng nhau bởi vạch chắn \(MN\). \(M,N\) lần lượt là trung điểm BC và AD. Một đội xây dựng làm một con đường đi từ A đến C qua vạch chắn MN, biết khi làm đường trên miền ABMN mỗi giờ làm được \(15\;{\rm{m}}\) và khi làm trong miền CDNM mỗi giờ làm được \(30\;{\rm{m}}\). Tính thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ \(A\) đến \(C\).

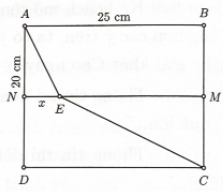
Do cần thời gian xây là ngắn nhất nên con đường làm trên mỗi miền phải là những đường thẳng.

Gọi AE và EC lần lượt là đoạn đường cần làm. Với \(NE = x(\;{\rm{m}})\).

\( \Rightarrow EM = 25 - x(\;{\rm{m}})\).

Ta được \(\left\{ {\begin{array}{*{20}{l}}{AE = \sqrt {A{N^2} + E{N^2}}  = \sqrt {100 + {x^2}} }\\{EC = \sqrt {M{C^2} + E{M^2}}  = \sqrt {100 + {{(25 - x)}^2}} }\end{array}} \right.\).

\( \Rightarrow \) Thời gian để làm đoạn đường từ \(A\) đến \(C\) là:

\(t(x) = \dfrac{{AE}}{{15}} + \dfrac{{EC}}{{30}} = \dfrac{{\sqrt {100 + {x^2}} }}{{15}} + \dfrac{{\sqrt {{{(25 - x)}^2} + 100} }}{{30}}(\;{\rm{h}}\)

\( \Rightarrow {t^\prime }(x) = \dfrac{x}{{15\sqrt {100 + {x^2}} }} - \dfrac{{25 - x}}{{30\sqrt {{{(25 - x)}^2} + 100} }}.\)

Xét \({t^\prime }(x) = 0 \Leftrightarrow \dfrac{x}{{15\sqrt {100 + {x^2}} }} - \dfrac{{25 - x}}{{30\sqrt {{{(25 - x)}^2} + 100} }} = 0\)

\( \Leftrightarrow 2x\sqrt {{{(25 - x)}^2} + 100}  = (25 - x)\sqrt {100 + {x^2}} \)

\( \Leftrightarrow 4{x^2}\left( {{{(25 - x)}^2} + 100} \right) = {(25 - x)^2}\left( {100 + {x^2}} \right)\)

\( \Leftrightarrow 4{x^2}{(25 - x)^2} + 400{x^2} - 100{(25 - x)^2} - {(25 - x)^2}{x^2} = 0\)

\( \Leftrightarrow 4{(25 - x)^2}\left( {{x^2} - 25} \right) + {x^2}\left( {{{20}^2} - {{(25 - x)}^2}} \right) = 0\)

\( \Leftrightarrow (x - 5)\left( {4{{(25 - x)}^2}(x + 5) + {x^2}(45 - x)} \right) = 0 \Leftrightarrow x = 5\)

Ta được \(t(0) = \dfrac{{4 + \sqrt {29} }}{6};t(5) = \dfrac{{2\sqrt 5 }}{3};t(25) = \dfrac{{1 + \sqrt {29} }}{3}\)

Vậy thời gian ngắn nhất mà đội xây dựng làm được con đương đi từ \(A\) đến \(C\) là \(\dfrac{{2\sqrt 5 }}{3}(\;{\rm{h}})\)