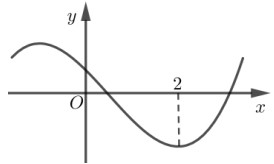
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Tìm \(m\) để bất phương trình \(f\left( x \right) \ge \dfrac{{x + 1}}{{x + 2}} + m\) nghiệm đúng với mọi \(x \in \left[ {0;\,\,1} \right].\)

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là

Công ty sữa Vinamilk thiết kế các sản phẩm dạng hình hộp chữ nhật có đáy là hình chữ nhật có chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Sản phẩm chứa dung tích bằng \(180{\rm{ml}}\). Khi thiết kế công ty luôn đặt ra mục tiêu sao cho vật liệu làm vỏ hộp là tiết kiệm nhất. Để công ty tiết kiệm được vật liệu nhất thì chiều dài của đáy hộp gần bằng giá trị nào sau đây?

Gọi \(m\) và \(M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = x - \sqrt {4 - {x^2}} .\) Khi đó \(M + m\) bằng

Cho hàm số \(f\left( x \right) = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\). Gọi \(M\) là giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 1;3} \right]\). Tổng các giá trị của tham số thực \(m\) để \(M = \dfrac{{71}}{2}.\)

Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán mỗi kg là \(40\;000\) đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng \(30\;{\rm{kg}}\). Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 4000 đồng thì số vải thiều bán được tăng thêm là \(40\;{\rm{kg}}\). Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kilôgam là 25000 đồng.

Trên đoạn [1 ; 5], hàm số \(y = x + \dfrac{4}{x}\) đạt giá trị nhỏ nhất tại điểm

Đề thi THPT QG 2019 – mã đề 104

Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 3x\) trên đoạn \(\left[ { - 3;3} \right]\) bằng