Biết rằng đồ thị hàm số bậc 4: \(y = f\left( x \right)\) được cho như hình vẽ sau:

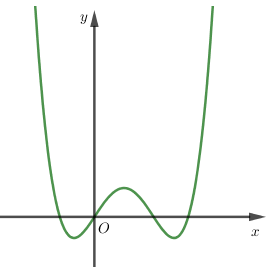
Tìm số giao điểm của đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) và trục $Ox.$

Đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại bốn điểm phân biệt nên \(f\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\)

\( \Rightarrow f'\left( x \right) = a\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_3}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_4}} \right)\) \( + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\)

Rõ ràng \(f\left( x \right) = 0 \Rightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\\x = {x_3}\\x = {x_4}\end{array} \right.\) \( \Rightarrow f'\left( x \right) \ne 0\) \( \Rightarrow g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f''\left( x \right).f\left( x \right) \ne 0\) nên ta chỉ xét \(f\left( x \right) \ne 0\)

\( \Rightarrow \dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = \dfrac{1}{{x - {x_1}}} + \dfrac{1}{{x - {x_2}}} + \dfrac{1}{{x - {x_3}}} + \dfrac{1}{{x - {x_4}}},\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}\)  

Đặt \(h\left( x \right) = \dfrac{{f'\left( x \right)}}{{f\left( x \right)}} = \dfrac{1}{{x - {x_1}}} + \dfrac{1}{{x - {x_2}}} + \dfrac{1}{{x - {x_3}}} + \dfrac{1}{{x - {x_4}}},\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}\)

Ta có $h'\left( x \right) = \dfrac{{f''\left( x \right).f\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{f^2}\left( x \right)}}$$ = \dfrac{{ - 1}}{{{{\left( {x - {x_1}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_2}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_3}} \right)}^2}}} + \dfrac{{ - 1}}{{{{\left( {x - {x_4}} \right)}^2}}} < 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$

$ \Rightarrow f''\left( x \right).f\left( x \right) - {\left[ {f'\left( x \right)} \right]^2} < 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$

$ \Rightarrow g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f''\left( x \right).f\left( x \right) > 0,\forall x \notin \left\{ {{x_1};{x_2};{x_3};{x_4}} \right\}$

Vậy đồ thị hàm số \(y = g\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} - f\left( x \right).f''\left( x \right)\) không cắt trục $Ox.$