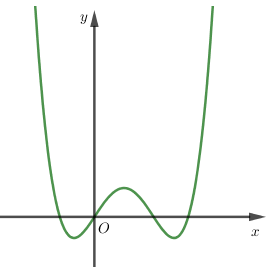
Cho hàm số $y = f(x)$ có đồ thị hàm số $f'(x)$ như hình vẽ. Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên khoảng
Trả lời bởi giáo viên
$y = f(1 - x) + \dfrac{{{x^2}}}{2} - x \Rightarrow y' = - f'(1 - x) + x - 1$
$\,y' < 0 \Leftrightarrow f'(1 - x) > - (1 - x)$
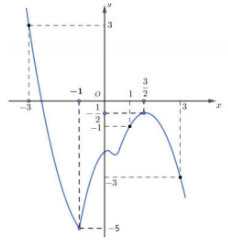
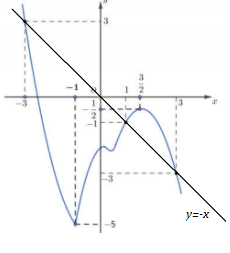
Dựa vào đồ thị hàm số, ta có: Đồ thị hàm số $f'(x)$ cắt đường thẳng $y = - x$ tại 3 điểm phân biệt là $A( - 3;3),\,\,B( - 1;1),\,\,C(3; - 3)$
$f'(1 - x) > - (1 - x) \Leftrightarrow \left[ \begin{array}{l}1 - x < - 3\\1 < 1 - x < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4\\ - 2 < x < 0\end{array} \right.$
Hàm số $y = f(1 - x) + \dfrac{{{x^2}}}{2} - x$ nghịch biến trên các khoảng $\left( { - 2;0} \right),\,\,\left( {4; + \infty } \right)$.
Hướng dẫn giải:
- Tính đạo hàm \(y'\) và tìm nghiệm của \(y'\) bằng cách vẽ đường thẳng \(y = - x\) trên cùng một phẳng tọa độ với đồ thị hàm số \(y = f'\left( x \right)\)
- Xét dấu đạo hàm \(y'\) vừa tính được ở trên và kết luận khoảng nghịch biến của hàm số.