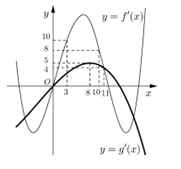
Cho hai hàm số \(y = f\left( x \right),\;y = g\left( x \right).\) Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right).\) Hàm số \(h\left( x \right) = f\left( {x + 6} \right) - g\left( {2x + \dfrac{5}{2}} \right)\) đồng biến trên khoảng nào dưới đây?
Trả lời bởi giáo viên
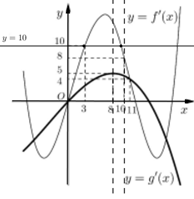
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 10\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại hai điểm phân biệt \(\left( {3;\;10} \right)\) và \(\left( {m;\;10} \right)\) với mọi \(m \in \left( {8;\;10} \right).\)
Ta có:
$f'\left( {x + 6} \right) \ge 10 \Leftrightarrow 3 \le x + 6 \le m < 10$ $ \Rightarrow - 3 \le x < 4$
$g'\left( {2x + \frac{5}{2}} \right) \le 5,\forall x \in R$
$\Rightarrow h'\left( x \right) = f'\left( {x + 6} \right) - 2g'\left( {2x + \frac{5}{2}} \right) $$\ge 10-2.5=0,\forall x \in \left[ { - 3;4} \right)$
Do đó hàm số h(x) đồng biến trên [-3;4)
Dựa vào các đáp án ta thấy đáp án B thỏa mãn.
Hướng dẫn giải:
- Tính đạo hàm \(h'\left( x \right)\)
- Hàm số \(y = h\left( x \right)\) đồng biến \( \Leftrightarrow h'\left( x \right) \ge 0.\)
- Tìm một khoảng mà $h(x)$ đồng biến rồi kiểm tra xem các khoảng ở mỗi đáp án có nằm trong khoảng vừa tìm được hay không rồi kết luận.