Cho hàm số $f\left( x \right) = {x^3} - 6{x^2} + 9x$. Đặt ${f^k}\left( x \right) = f\left( {{f^{k - 1}}\left( x \right)} \right)$ (với $k$ là số tự nhiên lớn hơn $1$). Tính số nghiệm của phương trình ${f^8}\left( x \right) = 0$

Ta có đồ thị hàm số $f\left( x \right) = {x^3} - 6{x^2} + 9x$ như sau:

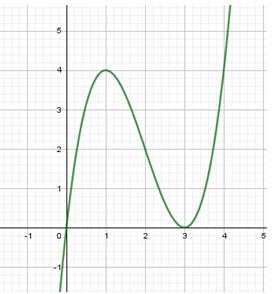
Dựa vào đồ thị hàm số ta có thể suy ra số nghiệm của phương trình $f\left( x \right) = m$ như sau:

$\left[ \begin{array}{l}m < 0\\m > 4\end{array} \right. \Rightarrow$ phương trình có $1$ nghiệm duy nhất.

$\left[ \begin{array}{l}m = 0\\m = 4\end{array} \right. \Rightarrow$ phương trình có $2$ nghiệm phân biệt.

$0 < m < 4 \Rightarrow$ phương trình có $3$ nghiệm phân biệt.

Xét phương trình ${f^2}\left( x \right) = 0 \Leftrightarrow {\left( {f\left( x \right)} \right)^3} - 6{\left( {f\left( x \right)} \right)^2} + 9f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 3\end{array} \right.$

Ta thấy phương trình $f\left( x \right) = 0$ có $2$ nghiệm phân biệt, phương trình $f\left( x \right) = 3$ có $3$ nghiệm phân biệt.

Vậy phương trình ${f^2}\left( x \right) = 0$ có $5$ nghiệm phân biệt

Xét phương trình ${f^3}\left( x \right) = 0 \Leftrightarrow f\left( {{f^2}\left( x \right)} \right) = 0 \Leftrightarrow {\left( {{f^2}\left( x \right)} \right)^3} - 6{\left( {{f^2}\left( x \right)} \right)^2} + 9{f^2}\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{f^2}\left( x \right) = 0\\{f^2}\left( x \right) = 3\end{array} \right.$

Phương trình ${f^2}\left( x \right) = 0$ có $2 + 3$ nghiệm phân biệt.

Phương trình ${f^2}\left( x \right) = 3 \Leftrightarrow {\left( {f\left( x \right)} \right)^3} - 6{\left( {f\left( x \right)} \right)^2} + 9f\left( x \right) = 3 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) \approx 3,88 \in \left( {0;4} \right)\\f\left( x \right) \approx 1,65 \in \left( {0;4} \right)\\f\left( x \right) \approx 0,46 \in \left( {0;4} \right)\end{array} \right.$

$\Rightarrow$ phương trình ${f^2}\left( x \right) = 3$ có $9$ nghiệm phân biệt.

Vậy phương trình ${f^3}\left( x \right) = 0$ có $2 + 3 + {3^2}$ nghiệm phân biệt.

Xét phương trình ${f^4}\left( x \right) = 0 \Leftrightarrow f\left( {{f^3}\left( x \right)} \right) = 0 \Leftrightarrow {\left( {{f^3}\left( x \right)} \right)^3} - 6{\left( {{f^3}\left( x \right)} \right)^2} + 9{f^3}\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{f^3}\left( x \right) = 0\\{f^3}\left( x \right) = 3\end{array} \right.$

Phương trình ${f^3}\left( x \right) = 0$ có $2 + 3 + {3^2}$ nghiệm phân biệt (cmt).

Phương trình

${f^3}\left( x \right) = 3 \Leftrightarrow {\left( {{f^2}\left( x \right)} \right)^3} - 6{\left( {{f^2}\left( x \right)} \right)^2} + 9{f^2}\left( x \right) = 3 \Leftrightarrow \left[ \begin{array}{l}{f^2}\left( x \right) \approx 3,88 \in \left( {0;4} \right)\\{f^2}\left( x \right) \approx 1,65 \in \left( {0;4} \right)\\{f^2}\left( x \right) \approx 0,46 \in \left( {0;4} \right)\end{array} \right.$

Ta thấy mỗi phương trình $f^2(x)=m$ ở trên có $9$ nghiệm phân biệt nên $3$ phương trình sẽ có $3.9=3^3$ nghiệm phân biệt.

Vậy phương trình ${f^4}\left( x \right) = 0$ có $2 + 3 + {3^2} + {3^3}$ nghiệm.

Cứ như vậy ta tính được phương trình ${f^8}\left( x \right) = 0$ có $2 + 3 + {3^2} + {3^3} + ... + {3^7} = 2 + \dfrac{{3\left( {1 - {3^7}} \right)}}{{1 - 3}} = 3281$ nghiệm.