Theo thống kê tại một nhà máy \(Z\), nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \dfrac{{95{x^2} + 120x}}{4}\), với \(x\) là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
Trả lời bởi giáo viên
\(x = 36\).
Bước 1: Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\). Biểu diễn các đại lượng khác theo t.
Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\) \( \Rightarrow \) số công nhân bỏ việc là \(\dfrac{t}{2}\) nên số công nhân làm việc là \(100 - \dfrac{t}{2}\) người.
Năng suất của công nhân còn \(120 - \dfrac{{5t}}{2}\) sản phẩm một giờ.
Số thời gian làm việc một tuần là \(40 + t = x\) giờ.
Bước 2: Lập hệ bất phương trình và tìm điều kiện của t.
Để nhà máy hoạt động được thì \(\left\{ {\begin{array}{*{20}{l}}{40 + t > 0}\\{120 - \dfrac{{5t}}{2} > 0 \Rightarrow t \in ( - 40;48)}\\{100 - \dfrac{t}{2} > 0}\end{array}} \right.\)
Bước 3: Biểu diễn số sản phẩm thu được theo t và khảo sát hàm số f(t).
Số sản phẩm trong một tuần làm được: \(S = \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t)\).
Số sản phẩm thu được là
\(f(t) = \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t) - \dfrac{{95{{(40 + t)}^2} + 120(40 + t)}}{4}\).
\({f^\prime }(t) = \)\( - \dfrac{1}{2}\left( {120 - \dfrac{{5t}}{2}} \right)(40 + t)\)\( - \dfrac{5}{2}\left( {100 - \dfrac{t}{2}} \right)(40 + t)\)\( + \left( {100 - \dfrac{t}{2}} \right)\left( {120 - \dfrac{{5t}}{2}} \right)\)\( - \dfrac{{95}}{2}(40 + t) - 30 = \)\(\dfrac{{15}}{4}{t^2} - \dfrac{{1135}}{2}t - 2330\)
Ta có \({f^\prime }(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = - 4}\\{t = \dfrac{{466}}{3}(\;{\rm{L}})}\end{array}} \right.\).
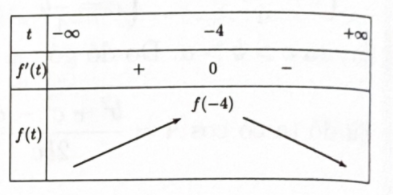
Bước 4: Tìm \(maxf\left( t \right)\) rồi tìm x.
Dựa vào bảng biến thiên ta có số lượng sản phẩm thu được mỗi tuần lớn nhất khi \(t = - 4 \Rightarrow x = 36\)
Hướng dẫn giải:
Bước 1: Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\). Biểu diễn các đại lượng khác theo t.
Bước 2: Lập hệ bất phương trình và tìm điều kiện của t.
Bước 3: Biểu diễn số sản phẩm thu được theo t và khảo sát hàm số f(t).
Bước 4: Tìm maxf(t) rồi tìm x.