Câu hỏi:
2 năm trước
Đề thi THPT QG 2019 – mã đề 104
Trong không gian \(Oxyz\) cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 5\). Có tất cả bao nhiêu điểm \(A\left( {a;b;c} \right)\) (a, b, c là các số nguyên) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho có ít nhất hai tiếp tuyến của \(\left( S \right)\) đi qua A và hai tiếp tuyến đó vuông góc với nhau ?
Trả lời bởi giáo viên
Đáp án đúng: c
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 5\) có tâm \(I\left( {0;0;1} \right)\), bán kính \(R = \sqrt 5 \).
Do \(A\left( {a;b;c} \right) \in Oxy \Rightarrow c = 0 \Rightarrow A\left( {x;y;0} \right)\).
Để từ A kẻ được ít nhất 2 tiếp tuyến vuông góc với nhau đến mặt cầu \(\left( S \right)\) thì \(R \le IA \le R\sqrt 2 \).
\( \Leftrightarrow \sqrt 5 \le \sqrt {{x^2} + {y^2} + {1^2}} \le \sqrt {10} \)\( \Leftrightarrow 4 \le {x^2} + {y^2} \le 9\), do đó tập hợp các điểm A là hình vành khăn (tính cả biên) giữa hai đường tròn \({x^2} + {y^2} = 4\) và \({x^2} + {y^2} = 9\).
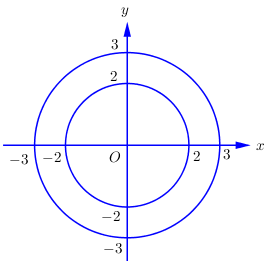
Ta có \(4 \le {x^2} + {y^2} \le 9\). Mà \(x,\,\,y \in \mathbb{Z} \Rightarrow {x^2} \le 9 \Rightarrow x \in \left\{ {0; \pm 1; \pm 2; \pm 3} \right\}\).
Ta có bảng giá trị:
Vậy có 20 điểm thỏa mãn yêu cầu bài toán.
