Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):x+y+z-1=0\), đường thẳng \(d:\frac{x-15}{1}=\frac{y-22}{2}=\frac{z-37}{2}\) và mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x-6y+4z+4=0\). Một đường thẳng \(\left( \Delta \right)\) thay đổi cắt mặt cầu \(\left( S \right)\) tại hai điểm \(A\), \(B\) sao cho \(AB=8\). Gọi \({A}'\), \({B}'\) là hai điểm lần lượt thuộc mặt phẳng \(\left( P \right)\) sao cho \(A{A}'\), \(B{B}'\) cùng song song với \(d\). Giá trị lớn nhất của biểu thức \(A{A}'+B{B}'\) là
Trả lời bởi giáo viên
Đáp án đúng: c
Hình vẽ tham khảo
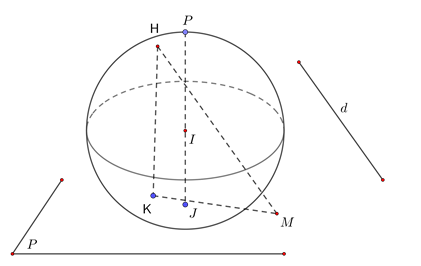
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 4;3;-2 \right)\) và bán kính \(R=5\).
Gọi \(H\) là trung điểm của \(AB\) thì \(IH\bot AB\) và \(IH=3\) nên \(H\) thuộc mặt cầu \(\left( {{S}'} \right)\) tâm \(I\) bán kính \({R}'=3\).
Gọi \(M\) là trung điểm của \({A}'{B}'\) thì \(A{A}'+B{B}'=2HM\), \(M\) nằm trên mặt phẳng \(\left( P \right)\).
Mặt khác ta có \(d\left( I;\left( P \right) \right)=\frac{4}{\sqrt{3}}<R\) nên \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) và \(\sin \left( d;\left( P \right) \right)=\sin \alpha =\frac{5}{3\sqrt{3}}\). Gọi \(K\) là hình chiếu của \(H\) lên \(\left( P \right)\) thì \(HK=HM.\sin \alpha \). Vậy để \(A{A}'+B{B}'\) lớn nhất thì \(HK\) lớn nhất
\(\Leftrightarrow HK\) đi qua \(I\) nên \(H{{K}_{\max }}={R}'+d\left( I;\left( P \right) \right)=3+\frac{4}{\sqrt{3}}=\frac{4+3\sqrt{3}}{\sqrt{3}}\).
Vậy \(A{A}'+B{B}'\) lớn nhất bằng \(2\left( \frac{4+3\sqrt{3}}{\sqrt{3}} \right).\frac{3\sqrt{3}}{5}=\frac{24+18\sqrt{3}}{5}\).
Hướng dẫn giải:
Dựng hình, biện luận vị trí điểm để tìm giá trị lớn nhất của tổng \(A{A}'+B{B}'\)
