Câu hỏi:
2 năm trước
Trong không gian Oxyz, cho mặt cầu \((S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-2z+5=0\). Phương trình mặt phẳng \((Q)\)chứa trục Ox và cắt \((S)\) theo giao tuyến là một đường tròn bán kính bằng 2 là
Trả lời bởi giáo viên
Đáp án đúng: d
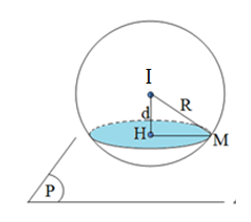
\((S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-2z+5=0\Leftrightarrow {{(x-3)}^{2}}+{{(y+2)}^{2}}+{{(z-1)}^{2}}=9\)
\(\Rightarrow \left( S \right)\) có tâm \(I(3;-2;1)\), bán kính \(R=3\).
\((Q)\) cắt \((S)\) theo giao tuyến là một đường tròn bán kính \(r=2\)
Ta có: \({{d}^{2}}+{{r}^{2}}={{R}^{2}}\Leftrightarrow {{d}^{2}}+{{2}^{2}}={{3}^{2}}\Leftrightarrow d=\sqrt{5}\)
Gọi \(\overrightarrow{n}(a;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là một VTPT của (Q). Khi đó \(\overrightarrow{n}\) vuông góc với VTCP \(\overrightarrow{u}(1;0;0)\)của Ox \(\Rightarrow 1.a+0.b+0.c=0\Leftrightarrow a=0\)
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT \(\overrightarrow{n}(0;b;c),\,\,\,\left( \overrightarrow{n}\ne \overrightarrow{0} \right)\) là:
\(0.(x-0)+b(y-0)+c(z-0)=0\Leftrightarrow by+cz=0\)
Khoảng cách từ tâm I đến (Q):
\(d=\frac{\left| b.(-2)+c.1 \right|}{\sqrt{{{b}^{2}}+{{c}^{2}}}}=\sqrt{5}\Rightarrow {{\left( 2b-c \right)}^{2}}=5({{b}^{2}}+{{c}^{2}})\Leftrightarrow {{b}^{2}}+4bc+4{{c}^{2}}=0\Leftrightarrow {{(b+2c)}^{2}}=0\Leftrightarrow b=-2c\)
Cho \(c=-1\Rightarrow b=2\Rightarrow \overrightarrow{n}(0;2;-1)\). Phương trình mặt phẳng (Q): \(2y-z=0\).
Hướng dẫn giải:
\({{d}^{2}}+{{r}^{2}}={{R}^{2}}\)
Trong đó,
\(d\): khoảng cách từ tâm O đến mặt phẳng (P),
\(r\): bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P),
\(R\): bán kính hình cầu.
