Trong các hàm số dưới đây, hàm số nào không đồng biến trên R?
+) Xét đáp án A:y=sinx−3x có: y′=cosx−3.
Với ∀x∈R ta có: −1≤cosx≤1⇒y′=cosx−3<0∀x∈R⇒ hàm số nghịch biến trên R.
Vậy hàm số ở đáp án A không đồng biến trên R.
+) Xét đáp án B: y=cosx+2x có: y′=−sinx+2.
Với ∀x∈R ta có: −1≤sinx≤1⇒y′=−sinx+2>0∀x∈R
Vậy hàm số đồng biến trên R.
+) Xét đáp án C: y′=3x2≥0,∀x nên hàm số đồng biến trên R.
+) Xét đáp án D: y′=5x4≥0,∀x nên hàm số đồng biến trên R.
Vậy chỉ có hàm số ở đáp án A không đồng biến trên R.
Cho hàm số y=f(x) nghịch biến và có đạo hàm trên (−5;5). Khi đó:
Vì y=f(x) nghịch biến trên (−5;5) nên f′(x)≤0,∀x∈(−5;5).
Vậy f′(0)≤0.
Cho hàm số y=f(x) xác định và liên tục trên R và có đạo hàm f′(x)=x2−4. Chọn khẳng định đúng:
Ta có: f′(x)=x2−4>0⇔[x>2x<−2 và f′(x)=x2−4<0⇔−2<x<2
Do đó hàm số đồng biến trên các khoảng (−∞;−2) và (2;+∞); nghịch biến trên khoảng (−2;2).
Cho hàm số y=f(x) có bảng biến thiên như sau:
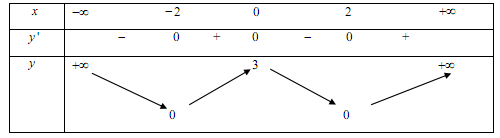
Khẳng định nào sau đây là khẳng định đúng:
A, B sai vì hàm số chỉ nghịch biến trên các khoảng (−∞;−2) và (0;2)
D sai vì hàm số chỉ đồng biến trên khoảng (−2;0) và (2;+∞)
C đúng vì giá trị thấp nhất của y trên bảng biến thiên là 0.
Trong tất cả các giá trị của tham số m để hàm số y=13x3+mx2−mx−m đồng biến trên R, giá trị nhỏ nhất của m là:
Ta có: y′=x2+2mx−m
Vì a=1>0 nên hàm số đồng biến trên R
⇔x2+2mx−m≥0,∀x∈R⇔Δ′=m2+m≤0⇔−1≤m≤0
Tìm các giá trị của tham số m sao cho hàm số y=−x3−x2+mx+1 nghịch biến trên R?
Ta có : y′=−3x2−2x+m
Để hàm số y là hàm số nghịch biến trên R thì y′≤0,∀x∈R ⇔−3x2−2x+m≤0,∀x∈R
⇔{−3<0Δ′=1+3m≤0⇔m≤−13.
Xác định giá trị của tham số m để hàm số y=x3−3mx2−m nghịch biến trên khoảng (0;1).
Ta có: y′=3x2−6mx⇒y′=0⇔x=0 hoặc x=2m
Trường hợp 1: m<0
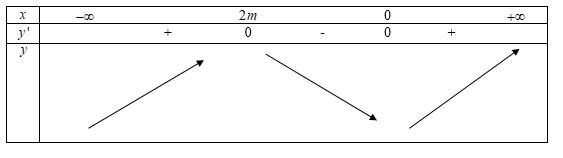
Dễ thấy hàm số trên khoảng (0;1) đồng biến với mọi m<0(loại)
Trường hợp 2: m=0
Với m=0 thì y′=3x2≥0 nên hàm số đồng biến trên R .
Do đó hàm số đồng biến trên (0;1) (loại)
Trường hợp 3: m>0
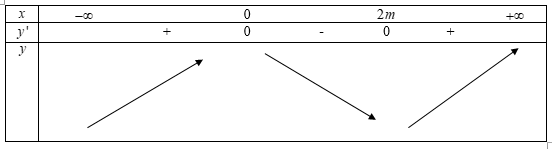
Dễ thấy hàm số trên khoảng (0;1) nghịch biến ⇔2m≥1⇔m≥12
Tìm m để hàm số y=x33−2mx2+4mx+2 nghịch biến trên khoảng (−2;0).
Ta có: y' = {x^2} - 4mx + 4m.
Hàm số nghịch biến trên \left( { - 2;0} \right) \Rightarrow y' \leqslant 0,\forall x \in \left( { - 2;0} \right) \Leftrightarrow {x^2} - 4mx + 4m \leqslant 0,\forall x \in \left( { - 2;0} \right) \Leftrightarrow {x^2} - 4m\left( {x - 1} \right) \leqslant 0 \Leftrightarrow 4m\left( {x - 1} \right) \geqslant {x^2} \Leftrightarrow 4m \leqslant \dfrac{{{x^2}}}{{x- 1}} (vì - 2 < x < 0)
Xét hàm g\left( x \right) = \dfrac{{{x^2}}}{{x - 1}} trên \left( { - 2;0} \right) ta có:
g'\left( x \right) = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \notin \left( { - 2;0} \right) \hfill \\x = 2 \notin \left( { - 2;0} \right) \hfill \\ \end{gathered} \right. \Rightarrow g'\left( x \right) > 0,\forall x \in \left( { - 2;0} \right)
Do đó hàm số y = g\left( x \right) đồng biến trên \left( { - 2;0} \right)
Suy ra g\left( { - 2} \right) < g\left( x \right) < g\left( 0 \right),\forall x \in \left( { - 2;0} \right) hay - \dfrac{4}{3} < g\left( x \right) < 0,\forall x \in \left( { - 2;0} \right)
Khi đó 4m \le g\left( x \right),\forall x \in \left( { - 2;0} \right) \Leftrightarrow 4m \le - \dfrac{4}{3} \Leftrightarrow m \le - \dfrac{1}{3}
Vậy m \leqslant - \dfrac{1}{3}
Cho hàm số y = f\left( x \right) có đạo hàm trên \mathbb{R} và bảng xét dấu của đạo hàm như hình vẽ sau

Có bao nhiêu số nguyên m \in \left( {0;2020} \right) để hàm số g\left( x \right) = f\left( {{x^2} - x + m} \right) nghịch biến trên khoảng \left( { - 1;0} \right)?
g\left( x \right) = f\left( {{x^2} - x + m} \right)
\Rightarrow g'\left( x \right) = \left( {2x - 1} \right).f'\left( {{x^2} - x + m} \right)
Với x \in \left( { - 1;0} \right) thì 2x - 1 < 0.
Do đó, để g\left( x \right) = f\left( {{x^2} - x + m} \right) nghịch biến trên khoảng \left( { - 1;0} \right) thì
\begin{array}{l}g'\left( x \right) \le 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left( {2x - 1} \right)f'\left( {{x^2} - x + m} \right) \le 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow f'\left( {{x^2} - x + m} \right) \ge 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - x + m \le 1\\{x^2} - x + m \ge 4\end{array} \right.,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - x \le 1 - m\\{x^2} - x \ge 4 - m\end{array} \right.,\forall x \in \left( { - 1;0} \right)\end{array}
Xét hàm h\left( x \right) = {x^2} - x trong \left( { - 1;0} \right) ta thấy:
h'\left( x \right) = 2x - 1 < 0,\forall x \in \left( { - 1;0} \right) nên hàm số nghịch biến trong \left( { - 1;0} \right)
\begin{array}{l} \Rightarrow h\left( { - 1} \right) > h\left( x \right) > h\left( 0 \right)\\ \Leftrightarrow 2 > h\left( x \right) > 0 \Leftrightarrow 0 < h\left( x \right) < 2\end{array}
Do đó
\begin{array}{l}\left[ \begin{array}{l}h\left( x \right) \le 1 - m\\h\left( x \right) \ge 4 - m\end{array} \right.,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l} 1 - m \ge \mathop {\max }\limits_{\left[ { - 1;0} \right]} h\left( x \right)\\ 4 - m \le \mathop {\min }\limits_{\left[ { - 1;0} \right]} h\left( x \right) \end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}1 - m \ge 2\\4 - m \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le - 1\\m \ge 4\end{array} \right.\end{array}
Mà m \in \left( {0;2020} \right),\,\,\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ {4;5;6;...;2019} \right\}: có 2016 giá trị.
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đạo hàm f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right) với mọi x \in \mathbb{R}. Có bao nhiêu số nguyên m thuộc đoạn \left[ { - 2019;\,2019} \right] để hàm số g\left( x \right) = f\left( {1 - x} \right) nghịch biến trên khoảng \left( { - \infty ;\, - 1} \right)?
Ta có:
g'\left( x \right) = \left[ {f\left( {1 - x} \right)} \right]' = \left( {1 - x} \right)'f'\left( {1 - x} \right)= - f'\left( {1 - x} \right)
= - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right] = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)
Hàm số g\left( x \right) nghịch biến trên \left( { - \infty ; - 1} \right)
\Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)
\Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right) (do x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right))
\Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge - m\,\,\forall x \in \left( { - \infty ; - 1} \right)
\Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right).
Ta có h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2.
BBT:
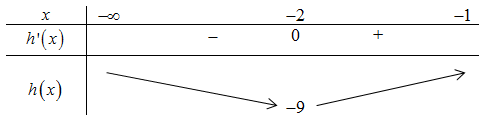
Dựa vào BBT ta có - m \le - 9 \Leftrightarrow m \ge 9.
Mà m \in \left[ { - 2019;2019} \right] và m nguyên nên m \in \left[ {9;10;11;...;2019} \right] hay có 2019 - 9 + 1 = 2011 giá trị của m thỏa mãn.
Cho f\left( x \right) mà đồ thị hàm số y = f'\left( x \right) như hình bên. Hàm số y = f\left( {x - 1} \right) + {x^2} - 2x đồng biến trên khoảng?
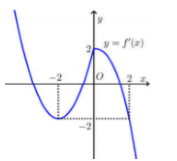
Ta có: y' = f'\left( {x - 1} \right) + 2x - 2 = 0 \Leftrightarrow f'\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0.
Đặt t = x - 1 ta có f'\left( t \right) + 2t = 0 \Leftrightarrow f'\left( t \right) - \left( { - 2t} \right) = 0.
Vẽ đồ thị hàm số y = f'\left( t \right) và y = - 2t trên cùng mặt phẳng tọa độ ta có:
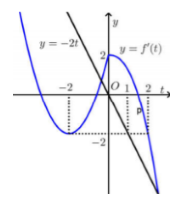
Xét y' \ge 0 \Leftrightarrow f'\left( t \right) \ge - 2t \Rightarrow Đồ thị hàm số y = f'\left( t \right) nằm trên đường thẳng y = - 2t.
Xét x \in \left( {1;2} \right) \Rightarrow t \in \left( {0;1} \right) \Rightarrow thỏa mãn.
Xét x \in \left( { - 1;0} \right) \Rightarrow t \in \left( { - 2; - 1} \right) \Rightarrow Không thỏa mãn.
Xét x \in \left( {0;1} \right) \Rightarrow t \in \left( { - 1;0} \right) \Rightarrow Không thỏa mãn.
Xét x \in \left( { - 2; - 1} \right) \Rightarrow t \in \left( { - 3; - 2} \right) \Rightarrow Không thỏa mãn.
Cho hàm số y = f\left( x \right) có đồ thị như hình bên:

Hàm số y = - 2f\left( x \right) đồng biến trên khoảng:
Dựa vào đồ thị hàm số ta có hàm số y = f\left( x \right) đồng biến trên các khoảng \left( { - \infty ;\,0} \right) và \left( {2;\, + \infty } \right).
Hàm số y = f\left( x \right) nghịch biến trên \left( {0;\,\,2} \right).
Xét hàm số: y = - 2f\left( x \right) ta có: y' = - 2f'\left( x \right).
Hàm số đồng biến \Leftrightarrow - 2f'\left( x \right) \ge 0 \Leftrightarrow f'\left( x \right) \le 0 \Leftrightarrow 0 \le x \le 2.
Vậy hàm số y = - 2f\left( x \right) đồng biến \Leftrightarrow x \in \left[ {0;\,2} \right].
Bất phương trình \sqrt {2{x^3} + 3{x^2} + 6x + 16} - \sqrt {4 - x} \geqslant 2\sqrt 3 có tập nghiệm là \left[ {a;b} \right]. Hỏi tổng a + b có giá trị là bao nhiêu?
ĐKXĐ : \left\{ \begin{gathered}2{x^3} + 3{x^2} + 6x + 16 \geqslant 0 \hfill \\4 - x \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}\left( {x + 2} \right)\left( {2{x^2} - x + 8} \right) \geqslant 0 \hfill \\4 - x \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow - 2 \leqslant x \leqslant 4
Tập xác định: D = \left[ { - 2;4} \right]
Xét hàm số
f(x) = \sqrt {2{x^3} + 3{x^2} + 6x + 16} - \sqrt {4 - x}
\Rightarrow f'(x) = \dfrac{{6{x^2} + 6x + 6}}{{2\sqrt {2{x^3} + 3{x^2} + 6x + 16} }} + \dfrac{1}{{2\sqrt {4 - x} }} > 0
Suy ra hàm số f(x) đồng biến trên tập xác định
Ta nhận thấy phương trình f\left( 1 \right) = 2\sqrt 3 \Rightarrow với x\ge 1 thì f\left( x \right) \geqslant f\left( 1 \right) = 2\sqrt 3 .
Suy ra tập nghiệm của bất phương trình là \left[ {1;4} \right].
Do đó tổng a + b = 5.
Tìm tất cả các giá trị thực của tham số m để hàm số y = \dfrac{{mx + 2}}{{2x + m}} nghịch biến trên từng khoảng xác định của nó?
Ta có y' = \dfrac{{{m^2} - 4}}{{{{\left( {2x + m} \right)}^2}}}.
Để hàm số đã cho nghịch biến thì y' < 0
\Leftrightarrow {m^2} - 4 < 0 \Rightarrow - 2 < m < 2
Tìm tất cả các giá trị thực của tham số m để trên \left( { - 1;1} \right), hàm số y = \dfrac{{mx + 6}}{{2x + m + 1}} nghịch biến.
y = \dfrac{{mx + 6}}{{2x + m + 1}} \Rightarrow y' = \dfrac{{m\left( {m + 1} \right) - 6.2}}{{{{\left( {2x + m + 1} \right)}^2}}} = \dfrac{{{m^2} + m - 12}}{{{{\left( {2x + m + 1} \right)}^2}}}
Hàm số nghịch biến trên \left( { - 1;1} \right)
\Leftrightarrow \left\{ \begin{array}{l}y' < 0\\\dfrac{{ - m - 1}}{2} \notin \left( { - 1;1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 12 < 0\\\left[ \begin{array}{l}\dfrac{{ - m - 1}}{2} \le - 1\\\dfrac{{ - m - 1}}{2} \ge 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 < m < 3\\\left[ \begin{array}{l} - m + 1 \le 0\\ - m - 3 \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 4 < m \le - 3\\1 \le m < 3\end{array} \right.
Cho hàm số đa thức f(x) có đạo hàm tràm trênR. Biếtf(0) = 0 và đồ thị hàm sốy = f'\left( x \right)như hình sau.
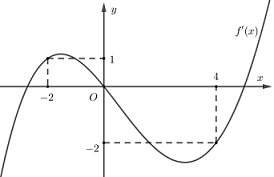
Hàm số g(x) = \left| {4f(x) + {x^2}} \right| đồng biến trên khoảng nào dưới đây ?
Đặt h\left( x \right) = 4f\left( x \right) + {x^2} ta có h'\left( x \right) = 4f\left( x \right) + 2x = 4\left[ {f'\left( x \right) + \dfrac{x}{2}} \right].
Số nghiệm của phương trình h'\left( x \right) = 0 là số giao điểm của đồ thị hàm số y = f'\left( x \right) và đường thẳng y = - \dfrac{x}{2}.
Vẽ đồ thị hàm số y = f'\left( x \right) và đường thẳng y = - \dfrac{x}{2} trên cùng mặt phẳng tọa độ ta có:
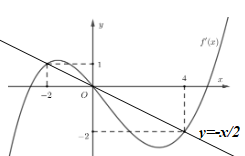
Dựa vào đồ thị hàm số ta thấy h'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\\x = 4\end{array} \right..
Khi đó ta có BBT hàm số y = h\left( x \right):
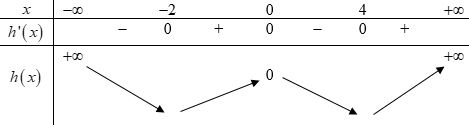
Khi đó ta suy ra được BBT hàm số g\left( x \right) = \left| {h\left( x \right)} \right| như sau:
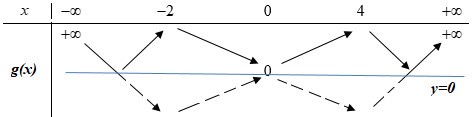
Dựa vào BBT và các đáp án ta thấy hàm số g\left( x \right) đồng biến trên \left( {0;4} \right).
Số giá trị nguyên của tham số m nhỏ hơn 10 để hàm số y=\left|3 x^{4}-4 x^{3}-12 x^{2}+m\right| nghịch biến trên khoảng (-\infty ;-1) là
5
5
5
Bước 1: Khảo sát hàm số f(x)=3 x^{4}-4 x^{3}-12 x^{2}+m
Xét hàm số f(x)=3 x^{4}-4 x^{3}-12 x^{2}+m \Rightarrow f^{\prime}(x)=12 x^{3}-12 x^{2}-24 x
Ta có f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=-1 \\ x=0 \\ x=2\end{array}\right.
Bảng biến thiên
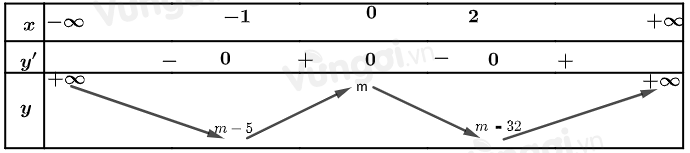
Bước 2: Tìm m để hàm số y=|f(x)| nghịch biến trên (-\infty ;-1)
Hàm số y=f(x) nghịch biến trên (-\infty ;-1)
Hàm số y=|f(x)| nghịch biến trên (-\infty ;-1) \Leftrightarrow m-5 \geq 0 \Leftrightarrow m \geq 5
Do m là số nguyên nhỏ hơn 10 nên ta có m \in\{5 ; 6 ; 7 ; 8 ; 9\}
Vậy có 5 giá trị m thỏa mãn yêu cầu bài toán
Cho hàm số y = \dfrac{{(4 - m)\sqrt {6 - x} + 3}}{{\sqrt {6 - x} + m}}. Số giá trị nguyên của m, trong khoảng (-10;10) sao cho hàm số đồng biến trên khoảng (-8; 5) là
14
14
14
Bước 1: Đặt t = \sqrt {6 - x} ,(t \ge 0), tính đạo hàm của f\left( t \right)
Đặt t = \sqrt {6 - x} ,(t \ge 0) khi đó ta có hàm số y = f(t) = \dfrac{{(4 - m)t + 3}}{{t + m}}.
Ta có: f'(t) = \dfrac{{ - {m^2} + 4m - 3}}{{{{(t + m)}^2}}}
Bước 2: Đánh giá t
Mặt khác hàm số y = \sqrt {6 - x} nghịch biến trên khoảng ( - \infty ;6) nên với - 8 < x < 5 thì f\left( { - 8} \right) < f\left( t \right) < f\left( 5 \right) \Leftrightarrow 1 < t < \sqrt {14}
Bước 3: Tìm m
Do đó hàm số y = \dfrac{{(4 - m)\sqrt {6 - x} + 3}}{{\sqrt {6 - x} + m}} đồng biến trên khoảng (-8 ; 5) khi và chỉ khi hàm số f(t) = \dfrac{{(4 - m)t + 3}}{{t + m}} nghịch biến trên khoảng (1;\sqrt {14} ). Khi đó
\begin{array}{l}f'(t) < 0,\forall t \in (1;\sqrt {14} )\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - {m^2} + 4m - 3 < 0}\\{ - m \notin (1;\sqrt {14} )}\end{array}} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ {\begin{array}{*{20}{l}}{m < 1}\\{m > 3}\end{array}} \right.\\\left[ {\begin{array}{*{20}{l}}{m \ge - 1}\\{m \le - \sqrt {14} }\end{array}} \right.\end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 3}\\{ - 1 \le m < 1}\\{m \le - \sqrt {14} }\end{array}} \right.\end{array}
Vì m nguyên, m \in ( - 10;10) nên
Với m>3 thì có m \in \left\{ {4;5;6;7;8;9} \right\}, có 6 giá trị
Với - 1 \le m < 1 thì có m \in \left\{ { - 1;0} \right\}, có 2 giá trị
Với m \le - \sqrt {14} \Rightarrow m \le - 4 thì có m \in \left\{ { - 9; - 8; - 7; - 6; - 5; - 4} \right\}, có 6 giá trị
Vậy có 14 giá trị nguyên của m thỏa mãn bài toán.
Cho hàm số y = f(x) liên tục và xác định trên \mathbb{R}, biết rằng {f^\prime }(x + 2) = {x^2} - 3x + 2. Hàm số y = f\left( {{x^2} + 4x + 7} \right) đồng biến trên khoảng nào dưới đây?
(1; + \infty ).
(1; + \infty ).
(1; + \infty ).
Bước 1: Giải {f^\prime }(x) = 0
Ta có {f^\prime }(x + 2) = {x^2} - 3x + 2 = (x - 1)(x - 2) = (x + 2 - 3)(x + 2 - 4)
\Rightarrow {f^\prime }(x) = (x - 3)(x - 4)
Khi đó {f^\prime }(x) = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = 4}\end{array}} \right..
Bước 2: Đặt y = g(x) = f\left( {{x^2} + 4x + 7} \right)
Đặt y = g(x) = f\left( {{x^2} + 4x + 7} \right)
Ta có: {g^\prime }(x) = (2x + 4) \cdot {f^\prime }\left( {{x^2} + 4x + 7} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x + 4 = 0}\\{{f^\prime }\left( {{x^2} + 4x + 7} \right) = 0}\end{array}} \right.
\Rightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{{x^2} + 4x + 7 = 3}\\{{x^2} + 4x + 7 = 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{{{(x + 2)}^2} = 0}\\{x = - 1}\\{x = - 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = - 1}\\{x = - 3}\end{array}} \right.} \right.
Bước 3: Xét dấu g'\left( x \right) và tìm khoảng đồng biến
Bảng xét dấu {g^\prime }(x).
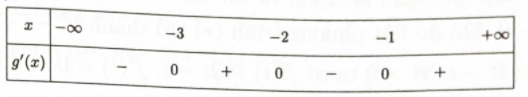
Dựa vào bảng xét dấu, ta có hàm số y = g(x) = f\left( {{x^2} + 4x + 7} \right) đồng biến trên khoảng (1; + \infty ).
Cho hàm số y = f(x) có đạo hàm liên tục trên ( - 1,3). Bảng biến thiên của hàm số y = {f^\prime }(x) được cho như hình vẽ dưới đây. Hàm số y = f\left( {1 - \dfrac{x}{2}} \right) + x nghịch biến trên khoảng nào sau đây?
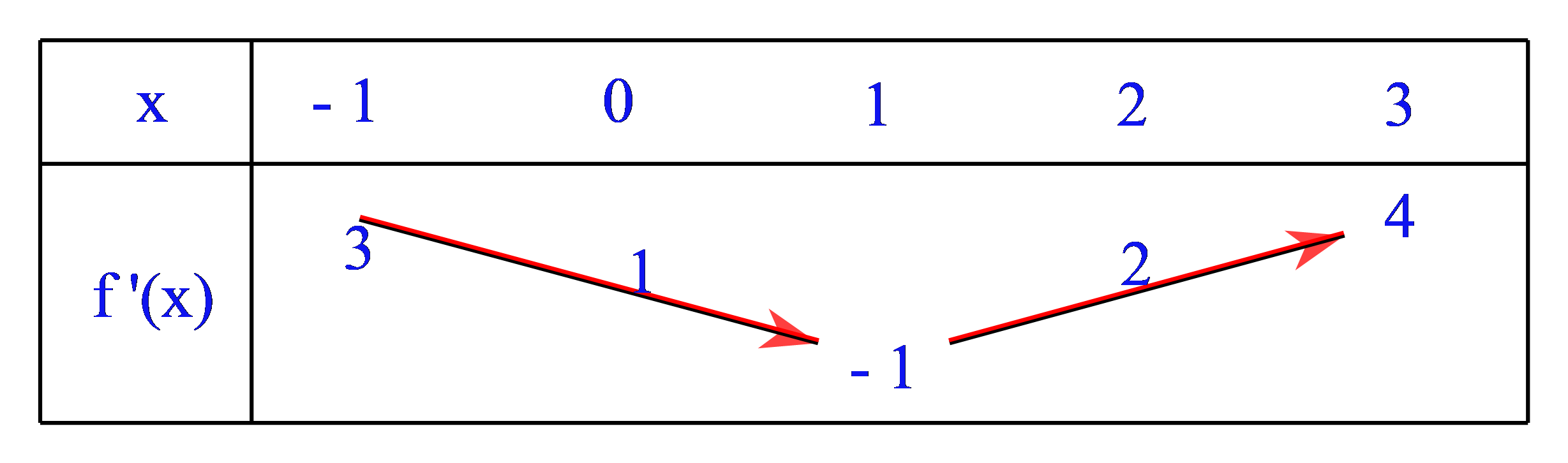
( - 4; - 2).
( - 4; - 2).
( - 4; - 2).
Ta có y = f\left( {1 - \dfrac{x}{2}} \right) + x \Rightarrow {y^\prime } = - \dfrac{1}{2}{f^\prime }\left( {1 - \dfrac{x}{2}} \right) + 1.
Xét {y^\prime } < 0 \Leftrightarrow - \dfrac{1}{2}{f^\prime }\left( {1 - \dfrac{x}{2}} \right) + 1 < 0 \Rightarrow 2 < {f^\prime }\left( {1 - \dfrac{x}{2}} \right) < 4 (dựa vào BBT)
\Leftrightarrow 2 < 1 - \dfrac{x}{2} < 3 \Leftrightarrow - 4 < x < - 2.
Dựa vào các đáp án nên hàm số y = f\left( {1 - \dfrac{x}{2}} \right) + x nghịch biến trên khoảng ( - 4; - 2).

