Xác định giá trị của tham số m để hàm số y=x3−3mx2−m nghịch biến trên khoảng (0;1).
Trả lời bởi giáo viên
Ta có: y′=3x2−6mx⇒y′=0⇔x=0 hoặc x=2m
Trường hợp 1: m<0
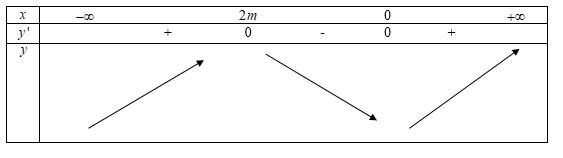
Dễ thấy hàm số trên khoảng (0;1) đồng biến với mọi m<0(loại)
Trường hợp 2: m=0
Với m=0 thì y′=3x2≥0 nên hàm số đồng biến trên R .
Do đó hàm số đồng biến trên (0;1) (loại)
Trường hợp 3: m>0
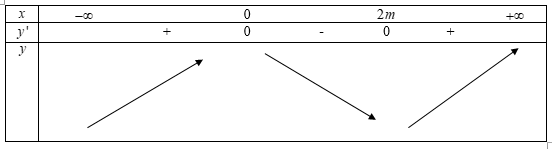
Dễ thấy hàm số trên khoảng (0;1) nghịch biến ⇔2m≥1⇔m≥12
Hướng dẫn giải:
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên D:
+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)≤0 với mọi x∈D
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.
+ Biện luận theo m để xét dấu đạo hàm.
- Bước 3: Kết luận.
Giải thích thêm:
Một số em sẽ bị nhầm khi cho rằng hàm số nghịch biến trên (0;1)⇔2m<1⇔m<12 dẫn đến chọn sai đáp án.
Có thể giải bài toán bằng cách khác:
Ở bước cho y′<0,∀x∈(0;1) ta có:
y′=3x2−6mx≤0,∀x∈(0;1)⇔m≥x2,∀x∈(0;1) (do x>0)
Lại có 0<x<1⇔0<x2<12 nên m≥x2,∀x∈(0;1)⇔m≥12.




