Câu hỏi:
2 năm trước
Cho hàm số đa thức f(x) có đạo hàm tràm trênR. Biếtf(0)=0 và đồ thị hàm sốy=f′(x)như hình sau.
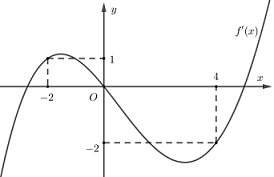
Hàm số g(x)=|4f(x)+x2| đồng biến trên khoảng nào dưới đây ?
Trả lời bởi giáo viên
Đáp án đúng: b
Đặt h(x)=4f(x)+x2 ta có h′(x)=4f(x)+2x=4[f′(x)+x2].
Số nghiệm của phương trình h′(x)=0 là số giao điểm của đồ thị hàm số y=f′(x) và đường thẳng y=−x2.
Vẽ đồ thị hàm số y=f′(x) và đường thẳng y=−x2 trên cùng mặt phẳng tọa độ ta có:
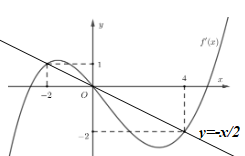
Dựa vào đồ thị hàm số ta thấy h′(x)=0⇔[x=−2x=0x=4.
Khi đó ta có BBT hàm số y=h(x):
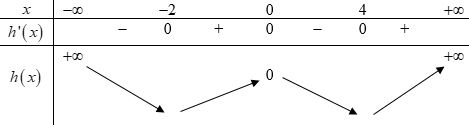
Khi đó ta suy ra được BBT hàm số g(x)=|h(x)| như sau:
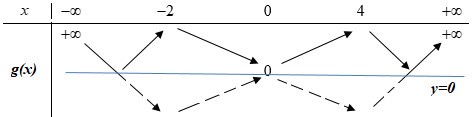
Dựa vào BBT và các đáp án ta thấy hàm số g(x) đồng biến trên (0;4).




