Cho hàm số \(y = f(x)\) liên tục và xác định trên \(\mathbb{R}\), biết rằng \({f^\prime }(x + 2) = {x^2} - 3x + 2\). Hàm số \(y = f\left( {{x^2} + 4x + 7} \right)\) đồng biến trên khoảng nào dưới đây?

Bước 1: Giải \({f^\prime }(x) = 0\)

Ta có \({f^\prime }(x + 2) = {x^2} - 3x + 2\)\( = (x - 1)(x - 2)\)\( = (x + 2 - 3)(x + 2 - 4)\)

\( \Rightarrow {f^\prime }(x) = (x - 3)(x - 4)\)

Khi đó \({f^\prime }(x) = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = 4}\end{array}} \right.\).

Bước 2: Đặt \(y = g(x) = f\left( {{x^2} + 4x + 7} \right)\)

Đặt \(y = g(x) = f\left( {{x^2} + 4x + 7} \right)\)

Ta có: \({g^\prime }(x) = (2x + 4) \cdot {f^\prime }\left( {{x^2} + 4x + 7} \right)\)\( = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x + 4 = 0}\\{{f^\prime }\left( {{x^2} + 4x + 7} \right) = 0}\end{array}} \right.\)

\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 2}\\{{x^2} + 4x + 7 = 3}\\{{x^2} + 4x + 7 = 4}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 2}\\{{{(x + 2)}^2} = 0}\\{x =  - 1}\\{x =  - 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 2}\\{x =  - 1}\\{x =  - 3}\end{array}} \right.} \right.\)

Bước 3: Xét dấu \(g'\left( x \right)\) và tìm khoảng đồng biến

Bảng xét dấu \({g^\prime }(x)\).

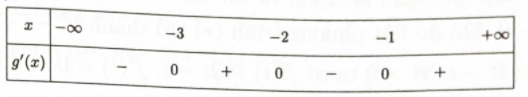
Dựa vào bảng xét dấu, ta có hàm số \(y = g(x) = f\left( {{x^2} + 4x + 7} \right)\) đồng biến trên khoảng \((1; + \infty )\).