Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)$ với mọi $x \in \mathbb{R}$. Có bao nhiêu số nguyên $m$ thuộc đoạn $\left[ { - 2019;\,2019} \right]$ để hàm số $g\left( x \right) = f\left( {1 - x} \right)$ nghịch biến trên khoảng $\left( { - \infty ;\, - 1} \right)$?

Ta có:

$g'\left( x \right)  = \left[ {f\left( {1 - x} \right)} \right]' = \left( {1 - x} \right)'f'\left( {1 - x} \right)=  - f'\left( {1 - x} \right)$

$=  - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]$ $=  - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)$

Hàm số $g\left( x \right)$ nghịch biến trên $\left( { - \infty ; - 1} \right)$

$\Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)$

$\Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)$ (do $x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)$)

$\Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge  - m\,\,\forall x \in \left( { - \infty ; - 1} \right)$

$\Leftrightarrow  - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)$.

Ta có $h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x =  - 2$.

BBT:

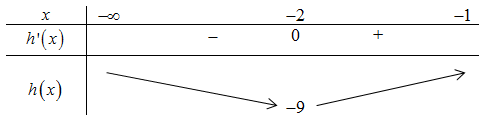
Dựa vào BBT ta có $- m \le  - 9 \Leftrightarrow m \ge 9$.

Mà $m \in \left[ { - 2019;2019} \right]$ và $m$ nguyên nên $m \in \left[ {9;10;11;...;2019} \right]$ hay có $2019 - 9 + 1 = 2011$ giá trị của $m$ thỏa mãn.