Câu hỏi:
2 năm trước
Cho hàm số \(y = f(x)\) có đạo hàm liên tục trên \(( - 1,3)\). Bảng biến thiên của hàm số \(y = {f^\prime }(x)\) được cho như hình vẽ dưới đây. Hàm số \(y = f\left( {1 - \dfrac{x}{2}} \right) + x\) nghịch biến trên khoảng nào sau đây?
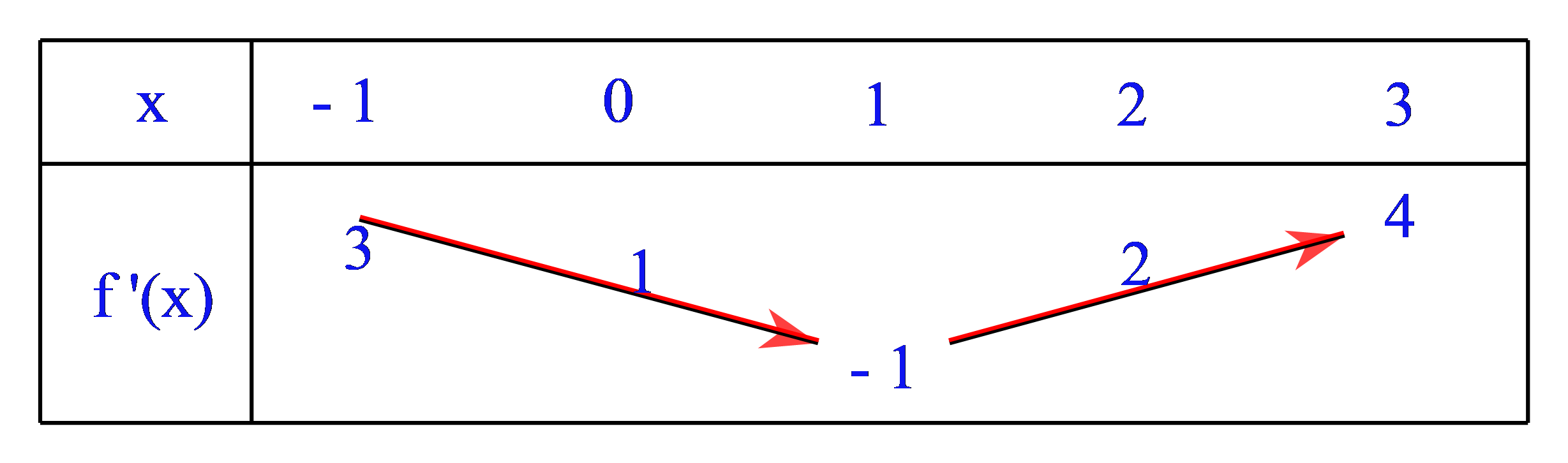
Trả lời bởi giáo viên
Đáp án đúng:
\(( - 4; - 2)\).
Ta có \(y = f\left( {1 - \dfrac{x}{2}} \right) + x\)\( \Rightarrow {y^\prime } = - \dfrac{1}{2}{f^\prime }\left( {1 - \dfrac{x}{2}} \right) + 1\).
Xét \({y^\prime } < 0 \Leftrightarrow - \dfrac{1}{2}{f^\prime }\left( {1 - \dfrac{x}{2}} \right) + 1 < 0\)\( \Rightarrow 2 < {f^\prime }\left( {1 - \dfrac{x}{2}} \right) < 4\) (dựa vào BBT)
\( \Leftrightarrow 2 < 1 - \dfrac{x}{2} < 3\)\( \Leftrightarrow - 4 < x < - 2\).
Dựa vào các đáp án nên hàm số \(y = f\left( {1 - \dfrac{x}{2}} \right) + x\) nghịch biến trên khoảng \(( - 4; - 2)\).
Hướng dẫn giải:
Bước 1: Tính đạo hàm
Bước 2: Giải \(y' < 0\) dựa vào bảng biến thiên.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
