Câu hỏi:
2 năm trước
Số giá trị nguyên của tham số $m$ nhỏ hơn 10 để hàm số $y=\left|3 x^{4}-4 x^{3}-12 x^{2}+m\right|$ nghịch biến trên khoảng $(-\infty ;-1)$ là
Trả lời bởi giáo viên
Đáp án đúng:
5
Bước 1: Khảo sát hàm số $f(x)=3 x^{4}-4 x^{3}-12 x^{2}+m$
Xét hàm số $f(x)=3 x^{4}-4 x^{3}-12 x^{2}+m \Rightarrow f^{\prime}(x)=12 x^{3}-12 x^{2}-24 x$
Ta có $f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x=-1 \\ x=0 \\ x=2\end{array}\right.$
Bảng biến thiên
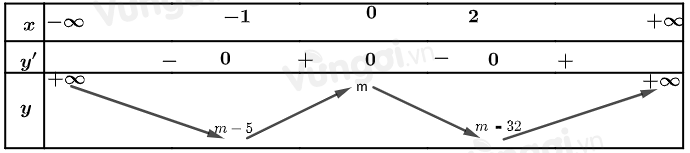
Bước 2: Tìm m để hàm số $y=|f(x)|$ nghịch biến trên $(-\infty ;-1)$
Hàm số y=f(x) nghịch biến trên $(-\infty ;-1) $
Hàm số $y=|f(x)|$ nghịch biến trên $(-\infty ;-1) \Leftrightarrow m-5 \geq 0 \Leftrightarrow m \geq 5$
Do $m$ là số nguyên nhỏ hơn 10 nên ta có $m \in\{5 ; 6 ; 7 ; 8 ; 9\}$
Vậy có 5 giá trị $m$ thỏa mãn yêu cầu bài toán
Hướng dẫn giải:
Bước 1: Khảo sát hàm số $f(x)=3 x^{4}-4 x^{3}-12 x^{2}+m$
Bước 2: Tìm m để hàm số $y=|f(x)|$ nghịch biến trên $(-\infty ;-1)$
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
