Phương trình logarit và một số phương pháp giải

$\left\{ \begin{array}{l}{\log _4}x.{\log _2}\left( {4x} \right) = {\log _{{2^2}}}x.\left( {2 + {{\log }_2}x} \right) = \dfrac{1}{2}{\log _2}x\left( {2 + {{\log }_2}x} \right) = t + \dfrac{1}{2}{t^2}\\{\log _{\sqrt 2 }}\left( {\dfrac{{{x^3}}}{2}} \right) = {\log _{{2^{\dfrac{1}{2}}}}}\left( {\dfrac{{{x^3}}}{2}} \right) = 2{\log _2}\left( {\dfrac{{{x^3}}}{2}} \right) = 2\left( {{{\log }_2}{x^3} - 1} \right) = 6{\log _2}x - 2 = 6t - 2\end{array} \right..$

Do đó phương trình đã cho trở thành $t + \dfrac{1}{2}{t^2} + 6t - 2 = 0 \Leftrightarrow {t^2} + 14t - 4 = 0$.

Phương trình $ \Leftrightarrow 9 - {2^x} = {2^{3 - x}} \Leftrightarrow 9 - {2^x} = \dfrac{8}{{{2^x}}}$

$ \Leftrightarrow {\left( {{2^x}} \right)^2} - {9.2^x} + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 1\\{2^x} = 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right..$

Điều kiện: \({3^{x + 1}} - 1 > 0 \Leftrightarrow x >  - 1.\)

Phương trình \( \Leftrightarrow {\log _3}\left( {{3^{x + 1}} - 1} \right) = 2x - {\log _3}2 \Leftrightarrow {\log _3}\left( {{3^{x + 1}} - 1} \right) + {\log _3}2 = 2x\)

\( \Leftrightarrow {\log _3}\left[ {\left( {{3^{x + 1}} - 1} \right).2} \right] = 2x\)\( \Leftrightarrow \left( {{3^{x + 1}} - 1} \right).2 = {3^{2x}} \Leftrightarrow {6.3^x} - 2 = {3^{2x}}\)

\( \Leftrightarrow {3^{2x}} - {6.3^x} + 2 = 0 \Rightarrow \left\{ \begin{array}{l}{3^{{x_1}}} + {3^{{x_2}}} = 6\\{3^{{x_1}}}{.3^{{x_2}}} = 2\end{array} \right..\)

Ta có \(S = {27^{{x_1}}} + {27^{{x_2}}}\) \( = {\left( {{3^{{x_1}}} + {3^{{x_2}}}} \right)^3} - {3.3^{{x_1}}}{.3^{{x_2}}}\left( {{3^{{x_1}}} + {3^{{x_2}}}} \right)\) \( = {6^3} - 3.2.6 = 180\)

Ta có: \({9^{{{\log }_3}\left( {{a^2}b} \right)}} = 4{a^3} \Leftrightarrow {3^{{{\log }_3}{{\left( {{a^2}b} \right)}^2}}} = 4{a^3}\) \( \Leftrightarrow {\left( {{a^2}b} \right)^2} = 4{a^3} \Leftrightarrow a{b^2} = 4\)

Điều kiện: \(x > 0\)

Đặt \(u = {\left( {2 + \sqrt 2 } \right)^{{{\log }_2}x}} > 0;\,\,\,v = {\left( {2 - \sqrt 2 } \right)^{{{\log }_2}x}} > 0.\)

Ta có: \(uv = {\left( {2 + \sqrt 2 } \right)^{{{\log }_2}x}}{\left( {2 - \sqrt 2 } \right)^{{{\log }_2}x}} = {\left[ {{2^2} - {{\left( {\sqrt 2 } \right)}^2}} \right]^{{{\log }_2}x}} = {2^{{{\log }_2}x}} = x.\)

Khi đó ta có phương trình đã cho trở thành: \(u + \left( {uv} \right)v = {u^2}{v^2} + 1 \Leftrightarrow \left( {u - 1} \right) + u{v^2} - {u^2}{v^2} = 0\)

\(\begin{array}{l} \Leftrightarrow \left( {u - 1} \right) - u{v^2}\left( {u - 1} \right) = 0\\ \Leftrightarrow \left( {u - 1} \right)\left( {1 - u{v^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}u = 1\\u{v^2} = 1\end{array} \right.\end{array}\)

+) Với \(u = 1 \Rightarrow {\left( {2 + \sqrt 2 } \right)^{{{\log }_2}x}} = 1 \Leftrightarrow {\log _2}x = 0 \Leftrightarrow x = 1\,\,\left( {tm} \right)\)

+) Với \(u{v^2} = 1 \Leftrightarrow uv.v = 1 \Rightarrow v = \dfrac{1}{x}\)

\( \Rightarrow {\left( {2 - \sqrt 2 } \right)^{{{\log }_2}x}} = \dfrac{1}{x} \Leftrightarrow {\log _2}{\left( {2 - \sqrt 2 } \right)^{{{\log }_2}x}} = {\log _2}\left( {\dfrac{1}{x}} \right)\)

\( \Leftrightarrow {\log _2}x.{\log _2}\left( {2 - \sqrt 2 } \right) =  - {\log _2}x\)

\( \Leftrightarrow {\log _2}x\left[ {{{\log }_2}\left( {2 - \sqrt 2 } \right) + 1} \right] = 0\)

\( \Leftrightarrow {\log _2}x = 0 \Leftrightarrow x = 1\,\,\,\,\left( {tm} \right)\)

Vậy \(x = 1\) là nghiệm của pt.

Điều kiện : $x \ne 2,{\mkern 1mu} {\mkern 1mu} x \ne {\rm{\;}} - 4$

$\begin{array}{l}{\log _4}\left( {{x^2} - 4x + 4} \right) + {\log _{16}}{\left( {x + 4} \right)^4} - m = 0 \\\Leftrightarrow {\log _4}{\left( {x - 2} \right)^2} + {\log _{16}}{\left( {x + 4} \right)^4} = m\\ \Leftrightarrow {\log _2}\left| {x - 2} \right| + {\log _2}\left| {x + 4} \right| = m \\\Leftrightarrow {\log _2}\left| {\left( {x - 2} \right)\left( {x + 4} \right)} \right| = m \\\Leftrightarrow \left| {{x^2} + 2x - 8} \right| = {2^m}\end{array}$

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số $y = \left| {{x^2} + 2x - 8} \right|$ và đường thẳng $y = {2^m}$.

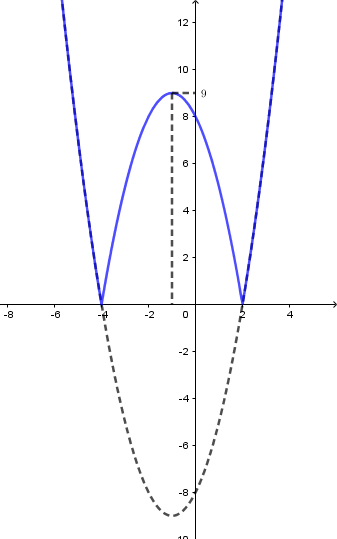
Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số $y = \left| {{x^2} + 2x - 8} \right|$ cắt đường thẳng $y = {2^m}$ tại 4 điểm phân biệt thì $0 < {2^m} < 9 \Leftrightarrow m < {\log _2}9 \Leftrightarrow m < 2{\log _2}3$.

Điều kiện: \({3^{x + 1}} - 1 > 0 \Leftrightarrow x >  - 1.\)

Phương trình \( \Leftrightarrow {\log _3}\left( {{3^{x + 1}} - 1} \right) = 2x - {\log _3}2\)\( \Leftrightarrow {\log _3}\left( {{3^{x + 1}} - 1} \right) + {\log _3}2 = 2x\)

\( \Leftrightarrow {\log _3}\left[ {\left( {{3^{x + 1}} - 1} \right).2} \right] = 2x\)\( \Leftrightarrow \left( {{3^{x + 1}} - 1} \right).2 = {3^{2x}} \Leftrightarrow {6.3^x} - 2 = {3^{2x}}\)

\( \Leftrightarrow {3^{2x}} - {6.3^x} + 2 = 0\)\( \Rightarrow \left\{ \begin{array}{l}{3^{{x_1}}} + {3^{{x_2}}} = 6\\{3^{{x_1}}}{.3^{{x_2}}} = 2\end{array} \right.\)

Ta có \(S = {27^{{x_1}}} + {27^{{x_2}}} = {\left( {{3^{{x_1}}} + {3^{{x_2}}}} \right)^3} - {3.3^{{x_1}}}{.3^{{x_2}}}\left( {{3^{{x_1}}} + {3^{{x_2}}}} \right)\) \( = {6^3} - 3.2.6 = 180\)

Điều kiện: \(x > 0,x \ne 1\)

Ta có:

$\dfrac{1}{{{{\log }_2}x}} + \dfrac{1}{{{{\log }_3}x}} + ... + \dfrac{1}{{{{\log }_{2019}}x}} = 2$\( \Leftrightarrow {\log _x}2 + {\log _x}3 + ... + {\log _x}2019 = 2\)

\( \Leftrightarrow {\log _x}\left( {2.3.4.....2019} \right) = 2\) \( \Leftrightarrow {x^2} = 2.3.4.....2019 = 2019!\)

Điều kiện: \(x > 0;x \ne 1\)

\({\log _{\sqrt 3 }}x + \dfrac{1}{{{{\log }_3}x}} = 3\)\( \Leftrightarrow 2{\log _3}x + \dfrac{1}{{{{\log }_3}x}} = 3\)

\( \Leftrightarrow 2\log _3^2x - 3{\log _3}x + 1 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \sqrt 3 \end{array} \right.\left( {TM} \right)\)

Vậy phương trình chỉ có \(1\) nghiệm hữu tỉ là \(x = 3\).

Ta có: ĐK: \(x > 2\)

${\log _3}x - {\log _3}(x - 2) = m$$ \Leftrightarrow {\log _3}\dfrac{x}{{x - 2}} = m \Leftrightarrow \dfrac{x}{{x - 2}} = {3^m}$

Xét hàm số \(f\left( x \right) = \dfrac{x}{{x - 2}}\) trên \(\left( {2; + \infty } \right)\) có \(f'\left( x \right) = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x > 2\)

Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2; + \infty } \right)\).

Bảng biến thiên:

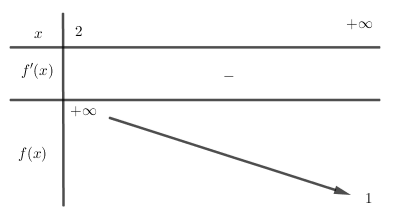
Do đó, phương trình đã cho có nghiệm \( \Leftrightarrow {3^m} > 1 \Leftrightarrow m > 0\).

Vậy giá trị nguyên nhỏ nhất của \(m\) thỏa mãn là \(m = 1\).

Điều kiện: $\dfrac{{{x^2} - 2x + 1}}{x} > 0 \Leftrightarrow \dfrac{{{{\left( {x - 1} \right)}^2}}}{x} > 0 \Leftrightarrow 0 < x \ne 1.$

Phương trình $ \Leftrightarrow {\log _3}\dfrac{{{{\left( {x - 1} \right)}^2}}}{x} + {x^2} - 2x + 1 = x$

$ \Leftrightarrow {\log _3}{\left( {x - 1} \right)^2} - {\log _3}x + {\left( {x - 1} \right)^2} = x$$ \Leftrightarrow {\log _3}{\left( {x - 1} \right)^2} + {\left( {x - 1} \right)^2} = {\log _3}x + x$        \(\left( * \right)\)

Xét hàm số $f\left( t \right) = {\log _3}t + t$ với $t > 0$. Ta có $f'\left( t \right) = \dfrac{1}{{t\ln 3}} + 1 > 0,{\rm{ }}\forall t > 0$.

Suy ra hàm số \(f\left( t \right)\) đồng biến trên \(\left( {0; + \infty } \right).\)

Nhận thấy \(\left( * \right)\) có dạng $f\left[ {{{\left( {x - 1} \right)}^2}} \right] = f\left( x \right)\, \Leftrightarrow {\left( {x - 1} \right)^2} = x$

$ \Leftrightarrow {x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{3 + \sqrt 5 }}{2}\left( {TM} \right)\\x = \dfrac{{3 - \sqrt 5 }}{2}\left( {TM} \right)\end{array} \right.$ $ \Rightarrow \dfrac{{3 + \sqrt 5 }}{2} + \dfrac{{3 - \sqrt 5 }}{2} = 3$

Ta có $\left( {x - \sqrt {{x^2} - 1} } \right)\left( {x + \sqrt {{x^2} - 1} } \right) = {x^2} - \left( {{x^2} - 1} \right) = 1$

Đặt $t\left( x \right) = x - \sqrt {{x^2} - 1} {\mkern 1mu} {\mkern 1mu} \left( {t > 0} \right) \Rightarrow x + \sqrt {{x^2} - 1}  = \dfrac{1}{t}$

Ta có $t'\left( x \right) = 1 - \dfrac{x}{{\sqrt {{x^2} - 1} }} = 0 \Leftrightarrow \sqrt {{x^2} - 1}  - x = 0$

Với $x > 2$ ta có $\sqrt {{x^2} - 1}  < \sqrt {{x^2}}  = x \Rightarrow \sqrt {{x^2} - 1}  - x < 0 \Rightarrow t'\left( x \right) < 0$$ \Rightarrow x > 2 \Rightarrow t \in \left( {0;2 - \sqrt 3 } \right)$

Khi đó phương trình trở thành 

\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {{\log }_2}t.{{\log }_5}t = {{\log }_m}{t^{ - 1}} =  - {{\log }_m}t{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\\{ \Leftrightarrow {{\log }_2}t.{{\log }_5}t + {{\log }_m}t = 0}\\{ \Leftrightarrow {{\log }_2}t.{{\log }_5}t + {{\log }_m}2.{{\log }_2}t = 0}\\{ \Leftrightarrow {{\log }_2}t\left( {{{\log }_5}t + {{\log }_m}2} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\log }_2}t = 0}\\{{{\log }_5}t + {{\log }_m}2 = 0}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 1{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\\{{{\log }_5}t =  - {{\log }_m}2 = {{\log }_m}\dfrac{1}{2}}\end{array}} \right. \Leftrightarrow t = {5^{{{\log }_m}\dfrac{1}{2}}}}\end{array}\)

Để phương trình ban đầu có nghiệm $x > 2$ thì phương trình (*) có nghiệm $t \in \left( {0;2 - \sqrt 3 } \right)$.

Điều kiện: $3{x^2} + 3x + m + 1 > 0$. Phương trình đã cho trở thành:

\(\begin{array}{l}\;\;\;\;\;{\log _2}\left( {\dfrac{{3{x^2} + 3x + m + 1}}{{2{x^2} - x + 1}}} \right) - 1 = {x^2} - 5x + 1 - m\\ \Leftrightarrow {\log _2}\dfrac{{3{x^2} + 3x + m + 1}}{{4{x^2} - 2x + 2}} = 4{x^2} - 3{x^2} - 2x - 3x + 2 - 1 - m\\ \Leftrightarrow {\log _2}\left( {3{x^2} + 3x + m + 1} \right) - {\log _2}\left( {4{x^2} - 2x + 2} \right) = \left( {4{x^2} - 2x + 2} \right) - \left( {3{x^2} + 3x + m + 1} \right)\\ \Leftrightarrow {\log _2}\left( {3{x^2} + 3x + m + 1} \right) + \left( {3{x^2} + 3x + m + 1} \right) = {\log _2}\left( {4{x^2} - 2x + 2} \right) + \left( {4{x^2} - 2x + 2} \right)\;\;\;\;\;\left( 1 \right)\end{array}\)

Xét hàm số: $f\left( t \right) = t + {\log _2}t$ trên $D = \left( {0; + \infty {\rm{ \;}}} \right)$, có $f'\left( t \right) = 1 + \dfrac{1}{{t.\ln 2}} > 0,\;\;\forall t \in D.$

Do đó hàm số $f\left( t \right)$ đồng biến trên $D$

$ \Rightarrow \left( 1 \right) \Leftrightarrow f\left( {4{x^2} - 2x + 2} \right) = f\left( {3{x^2} + 3x + m + 1} \right)$$ \Leftrightarrow 4{x^2} - 2x + 2 = 3{x^2} + 3x + m + 1 \Leftrightarrow {x^2} - 5x = m - 1\;\;\;\left( 2 \right)$

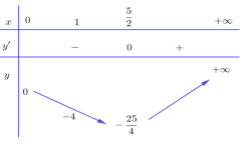
Xét hàm số: $g\left( x \right) = {x^2} - 5x$ trên $\mathbb{R}$, có

$g'\left( x \right) = 2x - 5 \Rightarrow g'\left( x \right) = 0 \Leftrightarrow x = \dfrac{5}{2}$.

Dựa vào bảng biến thiên ta thấy: phương trình $\left( 2 \right)$ có hai nghiệm phân biệt lớn hơn $1$ khi và chỉ khi

$ - \dfrac{{25}}{4} < m - 1 <  - {\mkern 1mu} 4 \Leftrightarrow  - \dfrac{{21}}{4} < m <  - {\mkern 1mu} 3$, do $m \in \mathbb{Z}$ nên $m \in \left\{ { - {\mkern 1mu} 5; - {\mkern 1mu} 4} \right\}.$

Điều kiện: $x > \dfrac{1}{2}$.

Phương trình \( \Leftrightarrow {\log _2}x.\left[ {{{\log }_3}\left( {2x - 1} \right) - 2} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}{\log _2}x = 0\\{\log _3}\left( {2x - 1} \right) = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\2x - 1 = 9\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {TM} \right)\\x = 5\left( {TM} \right)\end{array} \right. \Rightarrow {1^3} + {5^3} = 126.\)

Ta có

\(\begin{array}{*{20}{l}}{{e^x} + {e^{ - x}} = 2\cos ax + 4 \Leftrightarrow {{\left( {{e^{\frac{x}{2}}}} \right)}^2} + {{\left( {{e^{ - \frac{x}{2}}}} \right)}^2} - 2.{e^{\frac{x}{2}}}.{e^{ - \frac{x}{2}}} = 2\cos ax + 2}\\{ \Leftrightarrow {{\left( {{e^{\frac{x}{2}}} - {e^{ - \frac{x}{2}}}} \right)}^2} = 2\left( {\cos ax + 1} \right) = 2.2{{\cos }^2}\dfrac{{ax}}{2}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{e^{\frac{x}{2}}} - {e^{ - {\kern 1pt} \frac{x}{2}}} = 2\cos \dfrac{{ax}}{2} \left( 1 \right)}\\{{e^{\frac{x}{2}}} - {e^{ - {\kern 1pt} \frac{x}{2}}} =  - 2\cos \dfrac{{ax}}{2} \left( 2 \right)}\end{array}} \right..}\end{array}\)

Giả sử ${x_0}$ là nghiệm của phương trình ${e^x} - {e^{ - {\kern 1pt} x}} = 2\cos ax{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right),$ thì ${x_0} \ne 0$ và $2{x_0}$ là nghiệm của $\left( 1 \right)$ và $ - {\mkern 1mu} 2{x_0}$ là nghiệm của $\left( 2 \right)$ hoặc ngược lại.

Phương trình $\left( * \right)$ có 5 nghiệm nên hai phương trình $\left( 1 \right),{\mkern 1mu} {\mkern 1mu} \left( 2 \right)$ có 5 nghiệm phân biệt.

Vậy phương trình ${e^x} + {e^{ - {\kern 1pt} x}} = 2\cos ax + 4$ có 10 nghiệm phân biệt.

Bước 1: Đặt \(t = {\log _2}x\) và biến đổi phương trình bậc hai ẩn t.

Điều kiện: \(x > 0\).

Đặt \(t = {\log _2}x\) \( \Rightarrow x = {2^t}\).

Phương trình \(\log _2^2x - 3{\log _2}x + {m^2} - 5m + 8 = 0\) (1) trở thành \({t^2} - 3t + {m^2} - 5m + 8 = 0(2)\)

Bước 2: Tìm điều kiện để phương trình bậc hai ẩn t có 2 nghiệm phân biệt, từ đó biện luận m.

Phương trình (1) có hai nghiệm phân biệt \( \Leftrightarrow \)Phương trình (2) có hai nghiệm phân biệt \({t_1},{t_2}\).

Ta có \(\Delta  = 9 - 4\left( {{m^2} - 5m + 8} \right) > 0(*)\). Khi đó:

+) \({t_1} + {t_2} = 3\).

Ngoài ra, ta có: \(6 = {x_1} + {x_2} = {2^{{t_1}}} + {2^{{t_2}}}\)\( = {2^{{t_1}}} + {2^{3 - {t_1}}} = {2^{{t_1}}} + \dfrac{8}{{{2^{{t_1}}}}}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{2^{{t_1}}} = 2}\\{{2^{{t_1}}} = 4}\end{array}} \right. \Leftrightarrow \left[ \begin{array}{l}{t_1} = 1\\{t_1} = 2\end{array} \right.\left( 3 \right)\)

Mà \({t_1} + {t_2} = 3\) nên ta có

\(\left( 3 \right) \Leftrightarrow \left[ \begin{array}{l}{t_1} = 1,{t_2} = 2\\{t_1} = 2,{t_2} = 1\end{array} \right. \Leftrightarrow {t_1}.{t_2} = 2\)

\({t_1} \cdot {t_2} = 2 \Leftrightarrow {m^2} - 5m + 8 = 2\)\( \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = 3\end{array} \right.\left( {TM} \right)\)

Vậy tích các giá trị của m là 2.3=6.

${\log _3}(x + 2) + {\log _9}{(x + 2)^2} = \dfrac{5}{4}$ (*)

Đkxđ: $x >  - 2$

$(*) \Leftrightarrow {\log _3}(x + 2) + {\log _3}(x + 2) = \dfrac{5}{4} \Leftrightarrow {\log _3}(x + 2) = \dfrac{5}{8} $

$\Leftrightarrow x + 2 = {3^{\dfrac{5}{8}}} \Leftrightarrow x = \sqrt[8]{{{3^5}}} - 2(tm)$

${\log _3}\left( {2x - 1} \right) = 2 \Leftrightarrow 2x - 1 = {3^2} \Leftrightarrow 2x = 10 \Leftrightarrow x = 5$

Điều kiện $x \ge 1$

${\log _4}\left( {x - 1} \right) = 3 \Leftrightarrow x - 1 = {4^3} \Leftrightarrow x = 65$

Điều kiện : $x>1.$

\({\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 1} \right) = 3 \Leftrightarrow {\log _2}\left( {\left( {x - 1} \right).\left( {x + 1} \right)} \right) = 3 \)

$\Leftrightarrow {x^2} - 1 = {2^3} \Leftrightarrow x =  \pm 3$

So sánh với điều kiện suy ra $x=3$.