Có bao nhiêu số nguyên $m$ để phương trình ${\log _2}\dfrac{{3{x^2} + 3x + m + 1}}{{2{x^2} - x + 1}} = {x^2} - 5x + 2 - m$ có hai nghiệm phân biệt lớn hơn $1$.

Điều kiện: $3{x^2} + 3x + m + 1 > 0$. Phương trình đã cho trở thành:

$\begin{array}{l}\;\;\;\;\;{\log _2}\left( {\dfrac{{3{x^2} + 3x + m + 1}}{{2{x^2} - x + 1}}} \right) - 1 = {x^2} - 5x + 1 - m\\ \Leftrightarrow {\log _2}\dfrac{{3{x^2} + 3x + m + 1}}{{4{x^2} - 2x + 2}} = 4{x^2} - 3{x^2} - 2x - 3x + 2 - 1 - m\\ \Leftrightarrow {\log _2}\left( {3{x^2} + 3x + m + 1} \right) - {\log _2}\left( {4{x^2} - 2x + 2} \right) = \left( {4{x^2} - 2x + 2} \right) - \left( {3{x^2} + 3x + m + 1} \right)\\ \Leftrightarrow {\log _2}\left( {3{x^2} + 3x + m + 1} \right) + \left( {3{x^2} + 3x + m + 1} \right) = {\log _2}\left( {4{x^2} - 2x + 2} \right) + \left( {4{x^2} - 2x + 2} \right)\;\;\;\;\;\left( 1 \right)\end{array}$

Xét hàm số: $f\left( t \right) = t + {\log _2}t$ trên $D = \left( {0; + \infty {\rm{ \;}}} \right)$, có $f'\left( t \right) = 1 + \dfrac{1}{{t.\ln 2}} > 0,\;\;\forall t \in D.$

Do đó hàm số $f\left( t \right)$ đồng biến trên $D$

$\Rightarrow \left( 1 \right) \Leftrightarrow f\left( {4{x^2} - 2x + 2} \right) = f\left( {3{x^2} + 3x + m + 1} \right)$$\Leftrightarrow 4{x^2} - 2x + 2 = 3{x^2} + 3x + m + 1 \Leftrightarrow {x^2} - 5x = m - 1\;\;\;\left( 2 \right)$

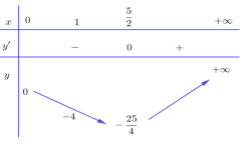
Xét hàm số: $g\left( x \right) = {x^2} - 5x$ trên $\mathbb{R}$, có

$g'\left( x \right) = 2x - 5 \Rightarrow g'\left( x \right) = 0 \Leftrightarrow x = \dfrac{5}{2}$.

Dựa vào bảng biến thiên ta thấy: phương trình $\left( 2 \right)$ có hai nghiệm phân biệt lớn hơn $1$ khi và chỉ khi

$- \dfrac{{25}}{4} < m - 1 <  - {\mkern 1mu} 4 \Leftrightarrow  - \dfrac{{21}}{4} < m <  - {\mkern 1mu} 3$, do $m \in \mathbb{Z}$ nên $m \in \left\{ { - {\mkern 1mu} 5; - {\mkern 1mu} 4} \right\}.$