Câu hỏi:
2 năm trước
Giá trị nguyên nhỏ nhất của tham số \(m\) để phương trình ${\log _3}x - {\log _3}(x - 2) = m$ có nghiệm là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: ĐK: \(x > 2\)
${\log _3}x - {\log _3}(x - 2) = m$$ \Leftrightarrow {\log _3}\dfrac{x}{{x - 2}} = m \Leftrightarrow \dfrac{x}{{x - 2}} = {3^m}$
Xét hàm số \(f\left( x \right) = \dfrac{x}{{x - 2}}\) trên \(\left( {2; + \infty } \right)\) có \(f'\left( x \right) = \dfrac{{ - 2}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x > 2\)
Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2; + \infty } \right)\).
Bảng biến thiên:
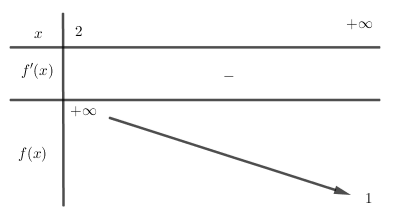
Do đó, phương trình đã cho có nghiệm \( \Leftrightarrow {3^m} > 1 \Leftrightarrow m > 0\).
Vậy giá trị nguyên nhỏ nhất của \(m\) thỏa mãn là \(m = 1\).
Hướng dẫn giải:
- Tìm điều kiện xác định của phương trình.
- Xét hàm số \(y = f\left( x \right)\) (ở đó \(f\left( x \right) = m\)) và tìm điều kiện để phương trình có nghiệm.
