Cho phương trình ${\log _4}\left( {{x^2} - 4x + 4} \right) + {\log _{16}}{\left( {x + 4} \right)^4} - m = 0$. Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.

Điều kiện : $x \ne 2,{\mkern 1mu} {\mkern 1mu} x \ne {\rm{\;}} - 4$

$\begin{array}{l}{\log _4}\left( {{x^2} - 4x + 4} \right) + {\log _{16}}{\left( {x + 4} \right)^4} - m = 0 \\\Leftrightarrow {\log _4}{\left( {x - 2} \right)^2} + {\log _{16}}{\left( {x + 4} \right)^4} = m\\ \Leftrightarrow {\log _2}\left| {x - 2} \right| + {\log _2}\left| {x + 4} \right| = m \\\Leftrightarrow {\log _2}\left| {\left( {x - 2} \right)\left( {x + 4} \right)} \right| = m \\\Leftrightarrow \left| {{x^2} + 2x - 8} \right| = {2^m}\end{array}$

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số $y = \left| {{x^2} + 2x - 8} \right|$ và đường thẳng $y = {2^m}$.

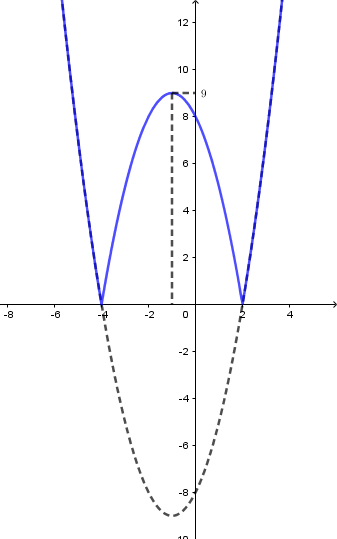
Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số $y = \left| {{x^2} + 2x - 8} \right|$ cắt đường thẳng $y = {2^m}$ tại 4 điểm phân biệt thì $0 < {2^m} < 9 \Leftrightarrow m < {\log _2}9 \Leftrightarrow m < 2{\log _2}3$.