Viết công thức công thức cộng vận tốc và nêu ý nghĩa của các đại lượng trong công thức.
- Công thức cộng vận tốc: \(\overrightarrow {{v_{1,3}}} = \overrightarrow {{v_{1,2}}} + \overrightarrow {{v_{2,3}}} \)
- Ý nghĩa của các đại lượng:
+ Vận tốc tuyệt đối \(\overrightarrow {{v_{1,3}}} \) là vận tốc của vật đối với hệ quy chiếu đứng yên.
+ Vận tốc tương đối \(\overrightarrow {{v_{1,2}}} \)là vận tốc của vật đối với hệ quy chiếu chuyển động.
+ Vận tốc kéo theo \(\overrightarrow {{v_{2,3}}} \)là vận tốc của hệ quy chiếu chuyển động đối với hệ quy chiếu đứng yên.
Một con thuyền đi dọc con sông từ bên A đến bên B cách nhau \(8km\) rồi quay ngay tại bến A mất thời gian \(2h\), tốc độ nước chảy không đổi bằng \(3km/h\). Tốc độ của thuyền so với nước là:
Khi thuyền đi xuôi dòng: \({v_x} = {v_{tn}} + 3\,\left( {km/h} \right)\)
Khi thuyền đi ngược dòng: \({v_n} = {v_{tn}} - 3\,\left( {km/h} \right)\)
Tổng thời gian đi là 2h nên ta có phương trình:
\(\begin{array}{l}\dfrac{8}{{{v_{tn}} + 3}} + \dfrac{8}{{{v_{tn}} - 3}} = 2\\ \Leftrightarrow 2v_{tn}^2 - 16{v_{tn}} - 18 = 0 \Rightarrow {v_{tn}} = 9km/h\end{array}\)
Một cano chạy thẳng đều xuôi theo dòng từ bến A đến bến B cách nhau \(36km\) mất một khoảng thời gian là \(1\) giờ \(30\)phút. Vận tốc của dòng chảy là \(6km/h\). Tính khoảng thời gian để cano chạy ngược dòng từ B đến A.
(1) Cano
(2) Dòng nước
(3) Bờ
Ta có:\(\left\{ \begin{array}{l}AB = 36km\\{v_{xuoi}} = \dfrac{{AB}}{{{t_{xuoi}}}} = \dfrac{{36}}{{1,5}} = 24km/h\\{v_{23}} = 6km/h\end{array} \right.\)
Vận tốc xuôi dòng:
\({v_{xuoi}} = {v_{12}} + {v_{23}}\)
\( \Rightarrow {v_{12}} = {v_{xuoi}} - {v_{23}} = 24 - 6 = 18km/h\)
Khi cano chạy ngược dòng, khi này vận tốc của cano so với bờ:
\({v_{nguoc}} = {v_{12}} - {v_{23}} = 18 - 6 = 12km/h\)
Thời gian ngược dòng từ B đến A là:
\({t_{nguoc}} = \dfrac{{AB}}{{{v_{nguoc}}}} = \dfrac{{36}}{{12}} = 3h\)
Vậy thời gian để cano chạy ngược dòng từ B đến A là 3 giờ.
Chọn phương án sai.
A, B, C - đúng
D – sai vì: Quỹ đạo và vận tốc của chuyển động đều có tính tương đối
Nếu xét trạng thái của một vật trong các hệ quy chiếu khác nhau thì điều nào sau đây là sai?
A, B, D – đúng
C – sai vì Quỹ đạo và vận tốc của chuyển động đều có tính tương đối còn hình dạng của vật không có tính tương đối.
Nhận xét nào sau đây của hành khách ngồi trên đoàn tàu đang chạy là đúng?
A – sai vì: Khi hành khách ngồi trên đoàn tàu đang chạy sẽ thấy cột đèn bên đường chuyển động so với toa tàu
B - sai vì: Khi hành khách ngồi trên đoàn tàu đang chạy sẽ thấy đầu tàu đứng yên so với toa tàu
C – đúng
D – sai vì: Người soát vé đang đi trên tàu chuyển động so với đầu tàu
Chọn khẳng định đúng. Đứng ở Trái Đất ta sẽ thấy:
Khi đứng ở Trái Đất ta sẽ thấy: Trái Đất đứng yên, Mặt Trời và Mặt Trăng quay quanh Trái Đất.
Khẳng định nào sau đây là đúng.
Từ công thức vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) , ta kết luận:
A – sai vì chiều của \(\overrightarrow {{v_{13}}} \) còn tùy thuộc vào phương chiều của cả \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \)
B – sai vì: \({v_{13}} = {v_{12}} + {v_{23}}\) nếu \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \) cùng phương, cùng chiều
C – sai vì: khi \(\overrightarrow {{v_{12}}} \) cùng phương, ngược chiều với \(\overrightarrow {{v_{23}}} \), \({v_{13}} = \left| {{v_{12}} - {v_{23}}} \right|\)
D – đúng
Khẳng định nào sau đây là đúng.
Từ công thức vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \) , ta kết luận:
A – sai vì chiều của \(\overrightarrow {{v_{13}}} \) còn tùy thuộc vào phương chiều của cả \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \)
B – sai vì: \({v_{13}} = {v_{12}} + {v_{23}}\) nếu \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \) cùng phương, cùng chiều
C – sai vì: khi \(\overrightarrow {{v_{12}}} \) cùng phương, ngược chiều với \(\overrightarrow {{v_{23}}} \), \({v_{13}} = \left| {{v_{12}} - {v_{23}}} \right|\)
D – đúng
Một xuồng máy chạy trên sông có vận tốc dòng chảy \(4m/s\). Động cơ của xuồng chạy với công suất không đổi và tính theo mặt nước, xuồng có vận tốc \(8m/s\). Vận tốc của xuồng tính theo hệ tọa độ gắn với bờ sông khi chạy xuôi dòng \({v_x}\) (vận tốc xuôi dòng) và \({v_{ng}}\) (vận tốc ngược dòng) có mối quan hệ với nhau như thế nào?
Hướng dẫn giải:
+ Vận tốc dòng chảy \({v_{23}} = 4m/s\)
+ Vận tốc xuồng so với nước: \({v_{12}} = 8m/s\)
- Khi xuồng chuyển động xuôi dòng: \({v_x} = {v_{12}} + {v_{23}} = 8 + 4 = 12m/s\)
- Khi xuồng chuyển động ngược dòng: \({v_{ng}} = {v_{12}} - {v_{23}} = 8 - 4 = 4m/s\)
\(\begin{array}{l} \Rightarrow \dfrac{{{v_x}}}{{{v_{ng}}}} = \dfrac{{12}}{4} = 3\\ \Rightarrow {v_x} = 3{v_{ng}}\end{array}\)
Một chiếc thuyền chạy ngược dòng nước từ \(A\) đến \(B\) mất \(6\) giờ, xuôi dòng mất \(4\) giờ. Nếu tắt máy để thuyền tự trôi theo dòng nước thì đi từ bến \(A\) đến bến \(B\) mất mấy giờ?
Ta có:
+ Thuyền (1) + Dòng nước (2) + Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}}\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
Thuyền tắt máy trôi theo dòng tương đương thuyền chuyển động với vận tốc \({v_{23}}\)
- Khi thuyền ngược dòng: \({v_{13}} = {v_{12}} - {v_{23}}\)
Khi xuôi dòng: \(v{'_{13}} = {v_{12}} + {v_{23}}\)
- Gọi \({t_1},{t_2}\) lần lượt là thời gian đi ngược dòng và đi xuôi dòng của thuyền, ta có:
\(\left\{ \begin{array}{l}{v_{13}} = \dfrac{{AB}}{{{t_1}}} = \dfrac{{AB}}{6}{\rm{ }}\left( 1 \right)\\v{'_{13}} = \dfrac{{AB}}{{{t_2}}} = \dfrac{{AB}}{4}{\rm{ }}\left( 2 \right)\end{array} \right.\)
Lấy \(\left( 1 \right) - \left( 2 \right) = 2{v_{23}} = \dfrac{{AB}}{{12}} \to {v_{23}} = \dfrac{{AB}}{{24}}\)
=> Nếu tắt máy để thuyền tự trôi theo dòng nước thì đi từ bến \(A\) đến bến \(B\) mất thời gian: \(t = \dfrac{{AB}}{{{v_{23}}}} = \dfrac{{AB}}{{\dfrac{{AB}}{{24}}}} = 24\) giờ
Một chiếc thuyền xuôi dòng từ \(A\) đến \(B\), vận tốc của dòng nước \(3,6km/h\). Tính chiều dài từ \(A\) đến \(B\) biết thuyền xuôi dòng mất \(2,5\) giờ và ngược dòng mất \(4\) giờ trên cùng đoạn đường AB?
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}}\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
- Khi xuôi dòng: \(v{'_{13}} = {v_{12}} + {v_{23}}\)
Khi thuyền ngược dòng: \({v_{13}} = {v_{12}} - {v_{23}}\)
- Gọi \({t_1},{t_2}\) lần lượt là thời gian đi xuôi dòng và đi ngược dòng của thuyền, ta có:
\(\left\{ \begin{array}{l}{t_1} = \dfrac{{AB}}{{{v_{13}}}} = \dfrac{{AB}}{{{v_{12}} + {v_{23}}}} = 2,5{\rm{ }}\left( 1 \right)\\{t_2} = \dfrac{{AB}}{{v{'_{13}}}} = \dfrac{{AB}}{{{v_{12}} - {v_{23}}}} = 4{\rm{ }}\left( 2 \right)\end{array} \right.\)
Từ (1) và (2), ta suy ra:
\(\begin{array}{l}\dfrac{{{v_{12}} - {v_{23}}}}{{{v_{12}} + {v_{23}}}} = \dfrac{{2,5}}{4}\\ \Rightarrow 8\left( {{v_{12}} - {v_{23}}} \right) = 5\left( {{v_{12}} + {v_{23}}} \right)\\ \Rightarrow 3{v_{12}} = 13{v_{23}}\\ \Rightarrow {v_{12}} = \dfrac{{13}}{3}{v_{23}} = \dfrac{{13}}{3}.3,6 = 15,6km/h\end{array}\)
Thế vào (1), ta được: \(AB = 2,5\left( {{v_{12}} + {v_{23}}} \right) = 2,5\left( {15,6 + 3,6} \right) = 48km\)
Một hành khách ngồi trên toa xe lửa đang chuyển động với vận tốc \(15m/s\) quan sát qua khe cửa thấy một đoàn tàu khác chạy cùng chiều trên đường sắt bên cạnh (coi xe lửa chạy nhanh hơn đoàn tàu). Từ lúc nhìn thấy điểm cuối đến lúc nhìn thấy điểm đầu của đoàn tàu mất hết \(8s\). Đoàn tàu người ấy quan sát gồm 20 toa, mỗi toa dài 4m. Tính vận tốc của đoàn tàu?
(1) xe lửa
(2) tàu
(3) mặt đường
Ta có:
+ Vận tốc của xe lửa so với đường: \({v_{13}} = 15m/s\)
+ Vận tốc của tàu so với đường: \({v_{23}} = ?\)
+ Vận tốc của xe lửa so với tàu: \({v_{12}}\)
Lại có: Từ lúc nhìn thấy điểm cuối đến lúc nhìn thấy điểm đầu của đoàn tàu mất hết \(8s\)
\( \Rightarrow {v_{12}}.t = 20.4\)
\( \Rightarrow {v_{12}} = \dfrac{{20.4}}{8} = 10m/s\)
Mặt khác, vận tốc của xe lửa so với đường: \({v_{13}} = {v_{12}} + {v_{23}}\)
\( \Rightarrow \) Vận tốc của tàu so với đường \({v_{23}} = {v_{13}} - {v_{12}} = 15 - 10 = 5m/s\)
Hai ô-tô chuyển động thẳng đều trên hai đoạn thẳng vuông góc với nhau. Vận tốc của ô-tô 1 là \(8m/s\), vận tốc của ô-tô 2 là \(6m/s\). Tính vận tốc của ô-tô 1 so với ô-tô 2
(1) ô-tô 1
(2) ô-tô 2
(3) mặt đất
Ta có:
+ \({v_{13}} = 8m/s\)
+ \({v_{23}} = 6m/s\)
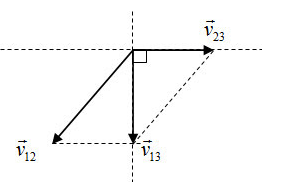
Từ hình ta suy ra: \({v_{12}} = \sqrt {v_{13}^2 + v_{23}^2} \)
\( \Rightarrow {v_{12}} = \sqrt {{8^2} + {6^2}} = 10m/s\)
Hai ô-tô cùng xuất phát từ hai bến xe A và B cách nhau 20km trên một đoạn đường thẳng. Nếu hai ô-tô chạy ngược chiều thì chúng sẽ gặp nhau sau \(15\) phút. Nếu hai ô-tô chạy cùng chiều thì chúng sẽ đuổi kịp nhau sau \(1\) giờ. Tính vận tốc của mỗi ô-tô.
(1) xe tại bến A
(2) xe tại bến B
(3) mặt đường
Ta có:
+ Thời gian gặp nhau khi 2 xe chạy ngược chiều: \({t_1} = 15p = 0,25h\)
+ Thời gian gặp nhau khi 2 xe chạy cùng chiều: \({t_2} = 1h\)
- Khi hai xe chuyển động ngược chiều, ta có: \({v_{12}} = {v_{13}} + {v_{23}} = \dfrac{{AB}}{{{t_1}}}\)
\( \Rightarrow {v_{13}} + {v_{23}} = \dfrac{{20}}{{0,25}} = 80\) (1)
- Khi hai xe chuyển động cùng chiều, ta có: \({v_{12}}' = {v_{13}} - {v_{23}} = \dfrac{{AB}}{{{t_2}}}\)
\( \Rightarrow {v_{13}} - {v_{23}} = \dfrac{{20}}{1} = 20\) (2)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{v_{13}} = 50km/h\\{v_{23}} = 30km/h\end{array} \right.\)
Ở một đoạn sông thẳng, dòng nước có vận tốc \({v_0}\), một người từ vị trí \(A\) ở bờ sông này muốn chèo thuyền tới vị trí \(B\) ở bờ sông bên kia. Cho \(AC = 6,CB = 8\). Độ lớn nhỏ nhất của vận tốc thuyền so với nước mà người này phải chèo đều để đến \(B\) là:
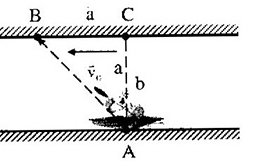
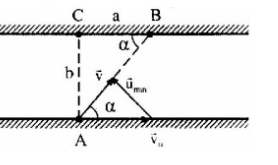
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}} = u\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}} = {v_0}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}} = v\)
- Vận dụng công thức cộng vận tốc, ta có: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \leftrightarrow \overrightarrow v = \overrightarrow u + \overrightarrow {{v_0}} \)
Để thuyền đến được điểm B thì \(\overrightarrow v \) phải có hướng \(\overrightarrow {AB} \).
Từ hình ta thấy, \({u_{\min }}\) khi \(\overrightarrow u \bot \overrightarrow v \)
Ta suy ra:
\(\begin{array}{l}\dfrac{{{u_{\min }}}}{{\sin {{90}^0}}} = \dfrac{{{v_0}}}{{\sin \alpha }}\\ \to {u_{\min }} = {v_0}\sin \alpha = {v_0}\dfrac{{AC}}{{AB}}\\ = {v_0}\dfrac{{AC}}{{\sqrt {A{C^2} + B{C^2}} }}\\ = {v_0}\dfrac{6}{{\sqrt {{6^2} + {8^2}} }} = 0,6{v_0}\end{array}\)
Vậy để thuyền đến được điểm B thì vận tốc thuyền so với nước nhỏ nhất phải là \({u_{\min }} = 0,6{v_0}\)
Một chiếc xe đang chạy với vận tốc \(36km/h\) trong mưa, giả sử mưa rơi thẳng đứng và đều đối với mặt đất. Người ngồi trên xe thấy các giọt mưa tạo một góc \({30^0}\) so với phương thẳng đứng. Vận tốc rơi của hạt mưa đối với đất có giá trị là:
Ta có:
+ Hạt mưa (1)
+ Xe (2)
+ Mặt đất (3)
+ \({v_{12}}\): vận tốc của hạt mưa so với xe
+ \({v_{23}} = 36km/h\): vận tốc của xe so với mặt đất
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên
- Vận dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Theo đầu bài ta có:
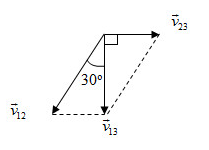
Từ hình, ta suy ra:
\(\begin{array}{l}\tan {30^0} = \dfrac{{{v_{23}}}}{{{v_{13}}}}\\ \to {v_{13}} = \dfrac{{{v_{23}}}}{{\tan {{30}^0}}}\\ = \dfrac{{36}}{{\dfrac{1}{{\sqrt 3 }}}} = 36\sqrt 3 km/h = 10\sqrt 3 m/s \approx 17,32m/s\end{array}\)
Một tàu hoả chuyển động thẳng đều với v = 10 m/s so với mặt đất. Một người đi đều trên sàn tàu có vận tốc 1m/s so với tàu. Xác định vận tốc của người đó so với mặt đất trong trường hợp người và tàu chuyển động vuông góc với nhau:
Cách giải:
Người và tàu chuyển động vuông góc với nhau nên vận tốc của người đó so với mặt đất là:
\({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} = \sqrt {{{10}^2} + {1^2}} = 10,05m/s\)
Một tàu hoả chuyển động thẳng đều với v = 10 m/s so với mặt đất. Một người đi đều trên sàn tàu có vận tốc 1m/s so với tàu. Xác định vận tốc của người đó so với mặt đất trong trường hợp người và tàu chuyển động ngược chiều:
Cách giải:
Chọn chiều dương là chiều chuyển động của tàu.
Người và tàu chuyển động ngược chiều nên vận tốc của người so với mặt đất là:
v13 = v23 – v12 = 10 – 1 = 9m/s
Một canô xuôi dòng từ bến A đến bến B mất 2 giờ, còn nếu đi ngược dòng từ bến B đến bến A hết 3 giờ. Biết dòng nước chảy với tốc độ 5 km/h. Độ lớn vận tốc của canô so với dòng nước là bao nhiêu?
Vật (1): cano; Vật (2): dòng nước; Vật (3): bờ sông.
Thời gian cano đi từ bến A đến bến B là: \(t = \dfrac{{AB}}{{{v_{13}}}}\)
+ Cano đi xuôi dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow \uparrow \,\,\overrightarrow {{v_{23}}} \)
→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}} = {v_{12}} + {v_{23}} = {v_{12}} + 5\,\,\left( {km/h} \right)\)
Thời gian đi xuôi dòng là: \({t_x} = \dfrac{{AB}}{{{v_{12}} + 5}} = 2\,\,\left( h \right)\,\,\,\,\,\,\,\,\left( * \right)\)
+ Cano đi ngược dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow \downarrow \,\,\overrightarrow {{v_{23}}} \,\,\,\left( {{v_{12}} > {v_{23}}} \right)\)
→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}}' = {v_{12}} - {v_{23}} = {v_{12}} - 5\,\,\left( {km/h} \right)\)
Thời gian đi ngược dòng là: \({t_n} = \dfrac{{AB}}{{{v_{12}} - 5}} = 3\,\,\left( h \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {**} \right)\)
Từ (1) và (2) ta có: \(\dfrac{{\left( * \right)}}{{\left( {**} \right)}} \Leftrightarrow \dfrac{{{v_{12}} - 5}}{{{v_{12}} + 5}} = \dfrac{2}{3} \Rightarrow {v_{12}} = 25\,\left( {km/h} \right)\)

