Chọn câu sai: Khi một chất điểm chuyển động thẳng biến đổi điều thì nó:
A, C, D - đúng
B - sai vì trong chuyển động biến đổi đều vận tốc thay đổi theo phương trình: \(v = {v_0} + at\)
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
Ta có: \(36km/h = 10m/s\)
+ Gia tốc của chuyển động: \(a = \frac{{10 - 0}}{{20}} = 0,5m/{s^2}\)
+ Phương trình vận tốc của vật: \(v = at = 0,5t\)
Thời gian để tàu đạt vận tốc \(54{\rm{ }}km/h = 15m/s\) tính từ lúc tàu đạt tốc độ 36km/h là: \(\Delta t = \frac{{15}}{{0,5}} - 20 = 30 - 20 = 10{\rm{s}}\)
Một vật đang chuyển động với vận tốc $36km/h$ , tài xế tắt máy và hãm phanh xe chuyển động chậm dần đều sau $50m$ nữa thì dừng lại. Quãng đường xe đi được trong $4s$ kể từ lúc bắt đầu hãm phanh là:
Gia tốc của chuyển động: \(a = \frac{{{0^2} - {{10}^2}}}{{2.50}} = - 1m/{s^2}\)
Quãng đường mà xe đi được trong 4 s kể từ lúc hãm phanh là: \(s = {v_0}t + \frac{1}{2}a{t^2} = 10.4 + \frac{1}{2}( - 1){.4^2} = 32m\)
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
Chất điểm chuyển động nhanh dần đều nếu a và v cùng dấu (a.v > 0)
=> Phương án C - sai vì: a.v0 < 0
Một vật chuyển động thẳng nhanh dần đều, trong giây thứ hai vật đi được quãng đường dài $1,5m$. Tính quãng đường vật đi được trong giây thứ $100$?
Gọi a là gia tốc của chuyển động
+ Vận tốc của vật sau giây thứ nhất là \({v_{01}} = a.1 = a\)
Quãng đường mà vật đi được trong giây thứ hai: \({s_2} = {v_{01}}t + \dfrac{1}{2}a{t^2} = a + \dfrac{a}{2} = 1,5{\rm{a = 1,5}} \to {\rm{a = 1m/}}{{\rm{s}}^2}\)
+ Vận tốc của vật sau giây thứ 99: \({v_{099}} = a.99 = 99m/s\)
Quãng đường vật đi được trong giây thứ 100: \({s_{100}} = {v_{099}}t + \dfrac{1}{2}a{t^2} = 99.1 + \dfrac{1}{2}1.1 = 99,5m\)
Gia tốc là đại lượng vật lý đặc trưng cho
Gia tốc là đại lượng vật lý đặc trưng cho khả năng thay đổi vận tốc (cả hướng và độ lớn) của vật và được xác định bằng biểu thức:
\(\overrightarrow a = \dfrac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{t - {t_0}}} = \dfrac{{\Delta \overrightarrow v }}{{\Delta t}}\)
Chọn phát biểu sai?
Trong chuyển động thẳng biến đổi đều thì
+ Gia tốc và vận tốc cùng phương, cùng chiều khi chuyển động này là nhanh dần đều
+ Gia tốc và vận tốc cùng phương, ngược chiều khi chuyển động này là chậm dần đều
Một vật chuyển động nhanh dần đều với vận tốc ban đầu $v_0 = 0$. Trong giây thứ nhất vật đi được quãng đường $s_1 = 3m$. Trong giây thứ hai vật đi được quãng đường $s_2$ bằng:
Chọn gốc tọa độ tại vị trí vật bắt đầu chuyển động
Gốc thời gian là lúc vật bắt đầu chuyển động
Ta có:
+ Phương trình chuyển động của vật là: $s = \dfrac{1}{2}a{t^2}$
+ Quãng đường vật đi được trong giây thứ nhất: \({s_1} = \dfrac{1}{2}a{.1^2} = 3 \to a = 6m/{s^2}\)
+ Quãng đường vật đi được trong hai giây đầu là \({s_2} = \dfrac{1}{2}{6.2^2} = 12m\)
=> Quãng đường vật đi được trong giây thứ 2 là: \(s = {s_2} - {s_1} = 12 - 3 = 9m\).
Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
Đổi \(54km/h = 15m/s\)
Gia tốc của xe:
\(a = \frac{{0 - 15}}{{10}} = - 1,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 15 - 1,5t\)
Vận tốc của xe sau khi hãm phanh 6 s là: \(v = 15 - 1,5.6 = 6m/s\)
Một xe ôtô chuyển động chậm dần đều với vận tốc ban đầu \(v_0= 20m/s\) và gia tốc \(3m/s^2\). Vận tốc của xe khi đi thêm \(50m\) và quãng đường đi được cho đến khi dừng lại hẳn lần lượt có giá trị là:
Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\)
Vận tốc của xe khi đi được quãng đường \(50 m\): \({v_1}^2 - v_0^2 = 2{\rm{a}}{{\rm{s}}_1} \to v = \sqrt {2{\rm{a}}{{\rm{s}}_1} + v_0^2} = \sqrt {2.( - 3).50 + {{20}^2}} = 10m/s\)
Quãng đường vật đi được cho đến khi dừng hẳn: \({v^2} - v_0^2 = 2{\rm{as}} \to s = \dfrac{{{v^2} - v_0^2}}{{2{\rm{a}}}} = \dfrac{{{0^2} - {{20}^2}}}{{2.( - 3)}} = 66,67m\)
Một đoàn tàu đang chạy với vận tốc 72km/h thì hãm phanh, chạy chậm dần đều sau 10s vận tốc giảm xuống còn 54km/h . Hỏi sau bao lâu thì tàu dừng lại hẳn
Gia tốc của xe : \(a = \frac{{15 - 20}}{{10}} = - 0,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 20 - 0,5t\)
Xe dừng lại hẳn khi: \(v = 0 \leftrightarrow 20 - 0,5t = 0 \to t = 40{\rm{s}}\)
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:
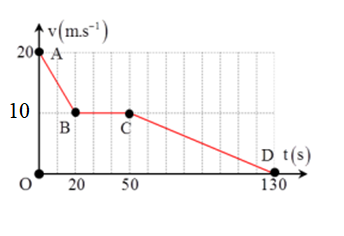
Quãng đường mà ôtô đi được là:
Ta có:
+ Trên đoạn \(A \to B\) xe chuyển động chậm dần đều với gia tốc: \({a_1} = \frac{{{v_B} - {v_A}}}{{\Delta t}} = \frac{{10 - 20}}{{20}} = - 0,5m/{s^2}\)
Quãng đường vật đi được: \({s_1} = 20t - 0,25{t^2} = 20.20 - 0,{25.20^2} = 300m\)
+ Trên đoạn \(B \to C\) xe chuyển động thẳng đều với vận tốc \(v = 10m/s\)
Quãng đường vật đi được: \({s_2} = vt = 10.30 = 300m\)
+ Trên đoạn \(C \to D\) xe chuyển động chậm dần đều với gia tốc:
\({a_3} = \frac{{0 - 10}}{{130 - 50}} = - 0,125m/s{}^2\)
Quãng đường vật đi được: \({s_3} = 10t - 0,0625{t^2} = 10.80 - 0,{0625.80^2} = 400m\)
Vậy quãng đường mà ôtô đi được là: \(s = {s_1} + {s_2} + {s_3} = 300 + 300 + 400 = 1000m\)
Cho đồ thị v - t của hai ôtô như hình vẽ:
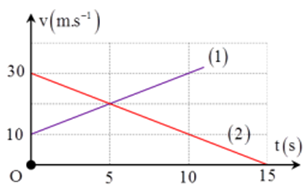
Giao điểm của đồ thị cho biết:
Giao điểm của đồ thị cho biết thời điểm 2 xe có cùng tốc độ
Chọn câu đúng?
Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
A - sai vì chuyển động thẳng đều có vận tốc không đổi
B - sai vì: \(a = 3,{v_0} = 0\) => vật chuyển động nhanh dần
C - sai vì \(a = - 2;{v_0} = 9\) => vật chuyển động chậm dần
D- đúng
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
Ta có: Vận tốc được xác định bằng biểu thức \(v = {v_0} + at\)
A, B, D - đúng
C -sai vì: \(v = {v_0} + at \to v = 2 + 4.2 = 10m/s\left( {{v_0} = 2,t = 2} \right)\)
Một xe chuyển động nhanh dần đều đi được S = 24m, S2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
Quãng đường vật đi được trong 2 khoảng thời gian liên tiếp bằng nhau là 4s là :
\(\begin{array}{l}{S_1}\; = {v_{01}}{t_1} + \frac{1}{2}a{t_1}^24.{v_{01}} + 8a = 24{\rm{ }}\left( 1 \right)\\{S_2} = {v_{02}}{t_2} + \frac{1}{2}a{t_2}^2\;4.{v_{01}} + 8a = 64{\rm{ }}\left( 2 \right)\end{array}\)
Mà \({v_{02}} = {v_1} = {v_{01}} + a{t_2}\left( 3 \right)\)
Giải (1), (2), (3) ta được : \({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
Hai người đi xe đạp khởi hành cùng một lúc từ 2 địa điểm A và B, đi ngược chiều nhau. Người đi từ A có vận tốc đầu là \(18km/h\) và chuyển động chậm dần đều với gia tốc \(20cm/{s^2}\). Người đi từ B có vận tốc đầu là \(5,4m/s\) và chuyển động nhanh dần đều với gia tốc\(0,2m/{s^2}\). Khoảng cách giữa hai người lúc đầu là \(130m\). Hỏi sau bao lâu 2 người gặp nhau và vị trí gặp nhau?
Chọn gốc tọa độ tại A, chiều dương là chiều từ A đến B, gốc thời gian là lúc hai người bắt đầu khởi hành.
Xe xuất phát từ A có:
\(\left\{ \begin{array}{l}{x_A} = 18km/h = 5m/s\\{a_A} = - 20cm/{s^2} = - 0,2m/{s^2}\\{x_{0A}} = 0\end{array} \right. \Rightarrow {x_A} = 5t - 0,1{t^2}\,\left( m \right)\)
Xe xuất phát từ B có:
\(\left\{ \begin{array}{l}{x_B} = - 5,4m/s\\{a_B} = - 0,2m/{s^2}\\{x_{0B}} = 130m\end{array} \right. \Rightarrow {x_B} = 130 - 5,4t - 0,1{t^2}\,\left( m \right)\)
Hai xe gặp nhau khi:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 5t - 0,1{t^2} = 130 - 5,4t - 0,1{t^2}\\ \Rightarrow t = 12,5s\end{array}\)
Thay \(t = 12,5s\) vào phương trình của \({x_A}\) ta được:
\({x_A} = 5.12,5 - 0,1.12,{5^2} = 46,875m\)
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
Đồ thị a - t của chất điểm chuyển động thẳng biến đổi đều có dạng là đường thẳng song song với trục Ot
Một ô tô đang chuyển động với vận tốc 54km/h thì hãm phanh chuyển động chậm dần đều đi được 20m thì vận tốc còn 18km/h. Tính gia tốc của ô tô và quãng đường ô tô đi được từ lúc hãm phanh đến lúc dừng hẳn.
Ta có: \(\left\{ \begin{array}{l}{v_0} = 54km/h = 15m/s\\v = 18km/h = 5m/s\\s = 20m\end{array} \right.\)
Áp dụng công thức liên hệ giữa s, v, a ta có:
\({v^2} - v_0^2 = 2a.s \Rightarrow a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{{5^2} - {{15}^2}}}{{2.20}} = - 5m/{s^2}\)
Khi ô tô dừng hẳn thì: \(v' = 0\)
Áp dụng công thức liên hệ giữa s’, v’, a ta có:
\(v{'^2} - {v^2} = 2a.s' \Rightarrow s' = \dfrac{{v{'^2} - {v^2}}}{{2a}} = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 5} \right)}} = 22,5m\)
Một vật chuyển động có đồ thị vận tốc như hình bên. Công thức vận tốc và công thức đường đi của vật là:
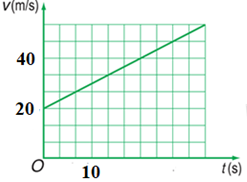
Biễu diễn số liệu như hình vẽ:
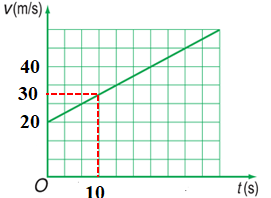
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{t_0} = 0;{v_0} = 20m/s\\{t_1} = 10s;{v_1} = 30m/s\end{array} \right.\)
Gia tốc của vật: \(a = \dfrac{{{v_1} - {v_0}}}{{{t_1} - {t_0}}} = \dfrac{{30 - 20}}{{10}} = 1m/{s^2}\)
Công thức vận tốc và quãng đường:
\(\left\{ \begin{array}{l}v = {v_0} + at = 20 + 1.t\\s = {v_0}t + \dfrac{1}{2}a{t^2} = 20.t + \dfrac{1}{2}.1.{t^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = 20 + t\,\,\left( {m/s} \right)\\s = 20t + \dfrac{{{t^2}}}{2}\,\left( m \right)\end{array} \right.\)

