Chuyển động thẳng đều là:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
Chọn phát biểu sai: Chuyển động thẳng đều là chuyển động của chất điểm trên một đường thẳng và:
A - sai vì : Chuyển động thẳng đều có vận tốc không đổi: \(v=const\)
B, C, D - đúng
Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng: \(x = 4 + 40t\)(x tính bằng km, t đo bằng giờ). Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu?
Áp dụng phương trình chuyển động thẳng đều: \(x = {x_0} + vt\)
ta có: \({x_0} = 4km\): chất điểm xuất phát từ điểm M cách O 1 đoạn 4km
phương trình chuyển động thẳng đều: \(x = {x_0} + vt\)
\( \Rightarrow v = 40\left( {km/h} \right)\)
Hai xe chạy ngược chiều đến gặp nhau, cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 120km. Vận tốc của xe đi từ A là 40km/h, của xe đi từ B là 20km/h.Thời điểm mà 2 xe gặp nhau là:
Chọn mốc tại A
ta có phương trình xe chuyển động từ A là: \({x_A} = {x_0} + {v_1}t = 40t\)
phương trình xe chuyển động từ B là: \({x_B} = {x_0}' + {v_2}t = 120 - 20t\)
Khi hai xe gặp nhau ta có: \({x_A} = {x_B}\)
\(\begin{array}{l} \Leftrightarrow 40t = 120 - 20t\\ \Rightarrow t = 2h\end{array}\)
Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng: \(x = -50 + 20t\) (x đo bằng km, t đo bằng h). Quãng đường chuyển động sau 2h là:
Ta có phương trình tọa độ: \(x = -50 + 20t\)
\( \Rightarrow v = 20\left( {km/h} \right)\)
Áp dụng công thức tính quãng đường ta có: \(s = v.t\)
sau 2h quãng đường chất điểm đi được là: \(s = 20.2 = 40\)km
Đồ thị vận tốc - thời gian của chuyển động thẳng đều là:
Trong chuyển động thẳng đều, vận tốc không thay đổi \(v = {v_0}\)
Suy ra: Đồ thị biểu diễn vận tốc theo thời gian là một đường thẳng song song với trục thời gian.
Lúc 7h sáng một người đi xe đạp đuổi theo một người đi bộ đã đi được 16 km. Cả hai chuyển động thẳng đều với vận tốc 12 km/h và 4 km/h. Người đi xe đạp đuổi kịp người đi bộ vào thời điểm và vị trí nào sau đây:
Chọn mốc là lúc 7h tại chỗ người đi xe xuất phát
Ta có:
phương trình chuyển động của người đi xe là: \[{x_1} = {x_0} + {v_1}t = 12t\]
phương trình chuyển động của người đi bộ là: \[{x_2} = {x_0} + {v_2}t = 16 + 4t\]
khi người đi xe đuổi kịp ta có: \({x_1} = {x_2}\)
\(\begin{array}{l} \Leftrightarrow 12t = 16 + 4t\\ \Rightarrow t = 2\left( h \right)\end{array}\)
vị trí của người đi xe khi đó so với mốc là: \({x_1} = {v_1}t = 12.2 = 24km\)
vậy hai người gặp nhau lúc 9h tại điểm cách nơi khởi hành 24km
Lúc 7h một oto chuyển động từ A đến B với vận tốc 80km/h. Cùng lúc một oto chuyển động từ B về A với vận tốc 80km/h. Biết khoảng cách từ A đến B là 200km, coi chuyển động của hai oto là chuyển động thẳng đều . Hai xe gặp nhau tại vị trí cách A là bao nhiêu? Khi đó đồng hồ chỉ mấy h?
Chọn chiều (+) là chiều từ A đến B, gốc thời gian là lúc 7h, gốc tọa độ tại điểm A
Phương trình chuyển động của 2 oto là:
\(\begin{array}{l}{x_1} = {x_{01}} + 80t\\{x_2} = {x_{02}} - 80t\end{array}\)
Tại thời điểm ban đầu: \({t_0} = 0\) (lúc đồng hồ chỉ 7h)
+ oto 1 đang ở A \( \to {x_{01}} = 0 \to {x_1} = 80t{\rm{ }}(km)\)
+ oto 2 đang ở B cách A 200km \( \to {x_{02}} = 200 \to {x_2} = 200 - 80t{\rm{ }}(km)\)
Hai xe gặp nhau khi: \({x_1} = {x_2} \leftrightarrow 80t = 200 - 80t \to t = 1,25h\)
Thay vào phương trình của xe 1, ta được vị trí gặp nhau: \(x = {x_1}(t = 1,25h) = 80.1,25 = 100(km)\)
=> Hai xe gặp nhau sau 1,25h (lúc 8,25h hay 8h15’) chuyển động và tại vị trí cách điểm A 100km, cách B 100km
Một oto chuyển động thẳng đều từ A đến B với vận tốc 90km/h. Sau 15phút từ B một xe máy chuyển động về A với vận tốc 40km/h. Sau khi đến B oto dừng lại nghỉ 30 phút rồi chuyển động thẳng đều quay trở lại A và gặp xe máy lần 2 ở điểm cách A là 25km (chưa đến A) . Độ dài quãng đường AB là:
Ta có:
+ 15phút = 0,25h, 30 phút = 0,5h
Chọn gốc thời gian là lúc xe máy bắt đầu đi, chiều dương từ A đến B, gốc tại A
Tọa độ gặp nhau lần thứ 2 của xe máy: \({x_2} = AB - 40t = 25 \to t = \frac{{AB - 25}}{{40}}{\rm{ (1)}}\)
Xe máy xuất phát sau oto 15phút, oto nghỉ 30 phút => trong quãng thời gian chuyển động của xe máy oto xuất phát chậm hơn 15phút = 0,25h
Tọa độ gặp nhau lần thứ 2 của oto:
\({x_1} = 2{\rm{A}}B - 90(t - 0,25) = 25{\rm{ (2)}}\)
Từ (1) và (2), ta có:
\(2AB - 90(\frac{{AB - 25}}{{40}} - 0,25) = 25 \to AB = 215(km)\)
Lúc 7 giờ, một người ở A chuyển động thẳng đều với v = 36 km/h đuổi theo người ở B đang chuyển động với v = 5 m/s. Biết AB = 18 km. Hai người gặp nhau lúc mấy giờ và cách A bao nhiêu kilomet?
Đổi: \(v = 5m/s = 18km/h\)
Chọn gốc toạ độ tại A, chiều dương là chiều chuyển động, gốc thời gian lúc 7 giờ.
Phương trình chuyển động của hai người là:
\(\left\{ \begin{array}{l}{x_A} = 36t\,\,\left( {km} \right){\rm{ }}\\{x_B} = {x_0} + {v_B}.t = 18 + 18t\,\,\left( {km} \right)\end{array} \right.\)
Hai người gặp nhau khi: \({x_A} = {x_B} \Leftrightarrow 36t = 18 + 18t \Rightarrow t = 1h\)
Vậy hai người gặp nhau lúc \(8h.\)
Vị trí hai người gặp nhau cách A: \({x_A} = 36.1 = 36km\)
Vào lúc 14h, hai oto chuyển động thẳng đều cùng chiều đi qua các thành phố A và B cách nhau 150km. Chiều chuyển động của các xe từ A đến B. Ôtô qua thành phố A có vận tốc 75km/h. Ôtô qua thành phố B có vận tốc 50 km/h. Hai xe gặp nhau tại vị trí cách B bao nhiêu km?
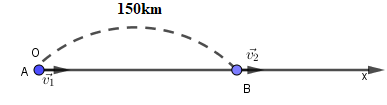
Chọn gốc tọa độ tại A, chiều dương chọn là chiều từ A hướng B. Chọn gốc thời gian là lúc 14h
Giả sử phương trình chuyển động của ô tô qua A có dạng:
\({x_A} = {x_{0A}} + {v_A}\left( {t - {t_{0A}}} \right)\)
Với: \(\left\{ \begin{array}{l}{x_{0A}} = 0\\{t_{0A}} = 0\\{v_A} = 75km/h\end{array} \right. \Rightarrow {x_A} = 0 + 75\left( {t - 0} \right) = 75t\,\,\left( {km} \right)\)
Giả sử phương trình chuyển động của ô tô qua B có dạng:
\({x_B} = {x_{0B}} + {v_B}\left( {t - {t_{0B}}} \right)\)
Với: \(\left\{ \begin{array}{l}{x_{0B}} = 150km\\{t_{0B}} = 0\\{v_B} = 50km/h\end{array} \right. \Rightarrow {x_B} = 150 + 50t\,\,\left( {km} \right)\)
Hai xe gặp nhau khi: \({x_A} = {x_B} \Rightarrow 75t = 150 + 50t \Rightarrow t = 6h\)
Thay t = 6h vào phương trình ta có: \({x_A} = 75.6 = 450\left( {km} \right)\)
Vị trí hai xe gặp nhau cách B: \(d = 450 - 150 = 300\left( {km} \right)\)

