Một người tập yoga. Tư thế đứng thứ nhất là đứng hai trên sàn, tư thế thứ 2 là đứng một chân trên mặt đất, tư thế thứ 3 là nằm trên sàn. Sự so sánh nào về áp lực và áp suất của người đó về các tư thế trên là đúng?
Áp lực do cùng một người tác dụng lên áp lực do 3 tư thế là như nhau.
Công thức tính áp suất: \(p = \dfrac{{{F_N}}}{S}\)
Cùng một áp lực, khi diện tích tiếp xúc càng lớn thì ấp suất sẽ càng nhỏ và ngược lại.
Tư thế thứ 3 có diện tích tiếp xúc lớn nhất nên có áp suất nhỏ nhất, sau đó là tư thế số 1 và cuối cùng là tư thế thứ 2.
Lực ma sát nghỉ xuất hiện khi:
Lực ma sát nghỉ \(({\overrightarrow F _{m{\rm{s}}n}})\) chỉ xuất hiện khi có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.
Biết thể tích các chất có trong các bình trong hình sau là như nhau, \({S_1} = {S_2} = {S_3} = 4{{\rm{S}}_4}\); \({\rho _{cátt}} = 3,6{\rho _{nuớc muối}} = 4{\rho _{nước}}\). Sự so sánh nào sau đây về áp lực của các chất trong bình tác dụng lên đáy bình là đúng?
Ta có công thức tính khối lượng riêng : \(\rho = \dfrac{m}{V}\)
\( \Rightarrow m = \rho .V\)
Mặt khác, áp lực sẽ được xác định bằng công thức: \({F_N} = P = m.g\)
Ta có: \({\rho _{cát}} = 3,6{\rho _{nước muối}} = 4{\rho _{nước}}\)và \(m = \rho .V\)
\( \Rightarrow {m_{cát}} > {m_{nước}} > {m_{nuớc muối}}\)
Từ đó, ta có: \({F_1} > {F_4} > {F_2} = {F_3}\)
Biết thể tích các chất có trong các bình trong hình sau là như nhau, \({S_1} = {S_2} = {S_3} = 4{{\rm{S}}_4}\); \({\rho _{cát}} = 3,6{\rho _{nước muối}} = 4{\rho _{nước}}\). Sự so sánh nào sau đây về áp suất của các chất trong bình tác dụng lên đấy bình là đúng?
Ta có công thức tính khối lượng riêng : \(\rho = \dfrac{m}{V}\)
\( \Rightarrow m = \rho .V\)
Mặt khác, áp lực sẽ được xác định bằng công thức: \({F_N} = P = m.g\)
Ta có: \({\rho _{cát}} = 3,6{\rho _{nước muối}} = 4{\rho _{nước}}\)và \(m = \rho .V\)
Từ đó có:
\(\begin{array}{l}{m_{cát}} > {m_{nước}} > {m_{nước muối}}\\{\rho _{nước}} = 0,9{\rho _{nước muối}}\end{array}\)
\( \Rightarrow {F_1} > {F_4} > {F_2} = {F_3}\)
Kết hợp với \({S_1} = {S_2} = {S_3} = 4{{\rm{S}}_4}\)
Ta có:
\(\begin{array}{l}{p_{cát}} = \dfrac{{{F_1}}}{{{S_1}}} = \dfrac{{{m_{cát}}.g}}{{4{{\rm{S}}_4}}} = \dfrac{{{\rho _{cát}}.V.g}}{{4{{\rm{S}}_4}}} = \dfrac{{3,6{\rho _{nước muối}}.V}}{{4{{\rm{S}}_4}}} = 0,9{p_4}(1)\\{p_{nước}} = \dfrac{{{F_2}}}{{{S_2}}} = \dfrac{{{m_{nước}}.g}}{{4{{\rm{S}}_4}}} = \dfrac{{{\rho _{nước}}.V.g}}{{4{{\rm{S}}_4}}} = \dfrac{{0.9.{\rho _{nước muối}}.V}}{{4{{\rm{S}}_4}}} = 0,225{p_4}(2)\end{array}\)
Từ (1) và (2) kết hợp với đáp án đề cho ta có: \({\rho _4} > {\rho _1} > {\rho _3} > {\rho _2}\)
Một vật có khối lượng m đặt ở nơi có gia tốc trọng trường g. Phát biểu nào sau đây sai?
A, B, D - đúng
C - sai vì: Trọng lực tỉ lệ thuận với khối lượng của vật.
Lực ma sát trượt xuất hiện:
Lực ma sát trượt \(({\overrightarrow F _{m{\rm{st}}}})\) xuất hiện ở mặt tiếp xúc khi hai vật trượt trên bề mặt của nhau.
Biết khối lượng của một khối đá là 15kg, gia tốc rơi tự do là 9,8 m/s2. Tính lực hút của khối đá lên Trái Đất.
Theo định luật III Newton, lực hút của hòn đá tác dụng lên Trái Đất bằng lực Trái Đất hút hòn đá, hay bằng trọng lượng của vật.
Ta có:
\(\begin{array}{l}F = P = m.g\\ \Rightarrow F = 15.9,8 = 147N\end{array}\)
Một vật có khối lượng $m$, ở độ cao $h$ so với mặt đất. Gọi $M$ là khối lượng Trái Đất, $G$ là hằng số hấp dẫn và $R$ là bán kính Trái Đất. Gia tốc rơi tự do tại vị trí đặt vật có biểu thức là:
Gia tốc rơi tự do: \(g = \dfrac{{GM}}{{{{(R + h)}^2}}}\)
Treo một vật nặng có khối lượng 0,2kg được treo vào một sợ dây không dãn. Xác định khối lượng của lực căng khi dây cân bằng. Lấy g = 9,8 m/s2.
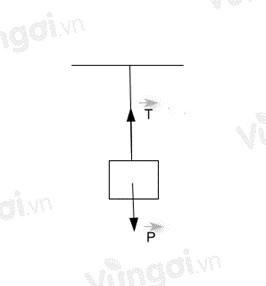
Theo định luật III Newton, lực căng khi treo dây bằng trọng lượng của vật.
Ta có:
\(\begin{array}{l}T = P = m.g\\ \Rightarrow F = 0,2.9,8 = 1,96N\end{array}\)
Tại cùng một địa điểm, hai vật có khối lượng \({m_1} < {m_2}\), trọng lượng tác dụng lên hai vật lần lượt là \({P_1},{P_2}\). Trọng lượng của hai vật đó luôn thỏa mãn điều kiện:
Ta có:
\(\begin{array}{l}{P_1} = {m_1}g\\{P_2} = {m_2}g\end{array}\)
Ta luôn có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{m_1}}}{{{m_2}}}\)
Nếu \({m_1} < {m_2}\)thì có \({P_1} < {P_2}\)
Một ngôi nhà gỗ có 8 cột đặt trên những viên đá hình vuông cạnh 40cm. Nền đất ở đây chỉ chịu được áp suất tối đa là 2.105 Pa. Để an toàn, người ta thiết kế cho áp suất ngôi nhà tác dụng lên nền đất chỉ bằng 50% áp suất trên. Hỏi ngôi nhà chỉ có thể có khối lượng tối đa là bao nhiêu? Lấy g = 10 m/s2.
Mỗi cột nhà được phép tác dụng lên nền nhà áp lực tối đa là:
\({F_c} = p.S = 0,{5.2.10^5}.0,4.0,4 = 0,{16.10^5}N\)
Nhà được phép tác dụng lên nền nhà lực tối đa là:
\(F = 8{F_c} = 8.0,{16.10^5} = 128000N\)
Do đó, khối lượng tối đa của nhà chỉ có thể có giá trị tối đa là 12800kg = 12, 8 tấn
Câu nào sau đây nhận xét sai khi nói về lực căng dây:
Lực căng là lực do sợi dây tác dụng vào vật, xuất hiện khi dây bị kéo căng, lò xo bị dãn.
Vậy nên, lực căng là chỉ là lực kéo.
Đo trọng lượng của một vật trên Trái Đất ta được P1 = 19,6 N. Tính khối lượng của vật, biết gia tốc rơi tự do của vật trên mặt đất là g = 9,8 m/s2
Ta có:
\(\begin{array}{l}P = m.g\\ \Rightarrow m = \dfrac{P}{g} = \dfrac{{19,6}}{{9,8}}\\ \Rightarrow m = 2(kg)\end{array}\)
Một ngọn đèn có khối lượng m = 1kg được treo dưới trần nhà bằng một sợi dây. Lấy g = 9,8 m/s2. Dây chỉ chịu được lực căng lớn nhất là 8N. Nếu treo ngọn đèn này vào một đầu dây thì:
Theo định luật III Newton, trọng lượng tác dụng lên vật bằng với lực căng dây tác dụng lên vật.
Ta có:
\(\begin{array}{l}T = P = m.g\\ \Rightarrow T = 1.9,8 = 9,8N\end{array}\)
Lực căng dây \(T = 9,8N > {T_{ma{\rm{x}}}} = 8N\), vậy nên dây sẽ bị đứt.
Có một vật làm bằng kim loại, khi treo vật đó vào một lực kế và nhúng chìm trong một bình tràn đựng nước thì lực kế chỉ 8,5 N đồng thời lượng nước tràn ra có thể tích 0,5 lít. Hỏi vật đó có khối lượng là bao nhiêu và làm bằng chất gì? Cho khối lượng riêng của nước là 1000 kg/m3.
Ta có thể tích nước tràn ra ngoài đúng bằng thể tích vật chiếm chỗ và bằng: \(V = 0,5l = 0,5{\rm{d}}{m^3} = {5.10^{ - 4}}{m^3}\)
Vật chịu tác dụng của trọng lực và lực đẩy Archimedes.
Lực đẩy Archimedes tác dụng lên vật là: \({F_A} = {\rho _n}Vg = {1000.5.10^{ - 4}}.10 = 5N\)
Trọng lượng của vật: \(P = F + {F_A} = 8,5 + 5 = 13,5N\)
Khối lượng của vật là: \(m = \dfrac{P}{{10}} = 1,35kg\)
Khối lượng riêng của vật: \(\rho = \dfrac{m}{V} = \dfrac{{1,35}}{{{{5.10}^{ - 4}}}} = 2700\left( {kg/{m^3}} \right)\)
vật đó là nhôm
Một vật khối lượng 2 kg, ở trên mặt đất có trọng lượng 20N. Khi chuyển vật tới một điểm cách tâm Trái Đất 2R (R là bán kính của Trái Đất) thì nó có trọng lượng bằng bao nhiêu?
Độ lớn của trọng lực: \(P = mg = G.\dfrac{{m.M}}{{{{\left( {R + h} \right)}^2}}}\)
Tại mặt đất: \(h = 0 \Rightarrow {P_1} = mg = G.\dfrac{{m.M}}{{{R^2}}}\)
Ở độ cao cách tâm Trái Đất một khoảng 2R: \( \Rightarrow h = R \Rightarrow {P_2} = mg = G.\dfrac{{m.M}}{{{{\left( {R + R} \right)}^2}}} = G.\dfrac{{m.M}}{{4{R^2}}}\)
Lấy: \(\dfrac{{{P_2}}}{{{P_1}}} = \dfrac{{G.\dfrac{{m.M}}{{4{R^2}}}}}{{G.\dfrac{{m.M}}{{{R^2}}}}} = \dfrac{1}{4} \Rightarrow {P_2} = \dfrac{{{P_1}}}{4} = \dfrac{{20}}{4} = 5N\)
Một toa tàu có khối lượng \(80\) tấn chuyển động thẳng đều dưới tác dụng của lực kéo nằm ngang \(F = {6.10^4}N\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Hệ số ma sát giữa tàu và đường ray là:
Ta có, toa tàu chuyển động thẳng đều => tổng các lực tác dụng lên toa tàu bằng 0
\(\overrightarrow F + \overrightarrow {{F_{m{\rm{s}}}}} = \overrightarrow 0 \) hay
\(\begin{array}{l}F = {F_{m{\rm{s}}}} \leftrightarrow F = \mu mg\\ \to \mu = \frac{F}{{mg}} = \frac{{{{6.10}^4}}}{{80000.10}} = 0,075\end{array}\)
Một đầu mát tạo ra lực kéo để kéo một toa xe có khối lượng \(5\) tấn, chuyển động với gia tốc \(0,3{\rm{ }}m/{s^2}\). Biết lực kéo của động cơ song song với mặt đường và hệ số ma sát giữa toa xe và mặt đường là \(0,02\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Lực kéo của đầu máy tạo ra là:
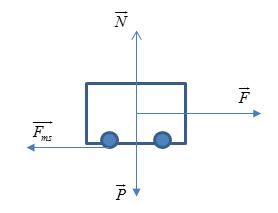
+ Các lực tác dụng lên xe gồm: Lực kéo \(\left( {\overrightarrow F } \right)\), lực ma sát \(\left( {\overrightarrow {{F_{m{\rm{s}}}}} } \right)\), trọng lực \(\left( {\overrightarrow P } \right)\), phản lực \(\left( {\overrightarrow N } \right)\)
+ Áp dụng định luật II-Niutơn, ta có: \(\overrightarrow F + \overrightarrow {{F_{m{\rm{s}}}}} + \overrightarrow P + \overrightarrow N = m\overrightarrow a \)
Chọn chiều dương trùng chiều chuyển động
Chiếu theo các phương ta được:
- Theo phương Oy: \(P = N\)
- Theo phương Ox: \(F - {F_{m{\rm{s}}}} = ma\)
\(\begin{array}{l} \to F = ma + {F_{m{\rm{s}}}} = ma + \mu N\\ \to F = ma + \mu mg = 5000.0,3 + 0,02.10.5000\\ = 2500N\end{array}\)
Một vận động viên môn hốc cây (môn khúc quân cầu) dùng gậy gạt quả bóng để truyền cho nó một tốc độ đầu 10m/s. Hệ số ma sát trượt giữa quả bóng với mặt băng là 0,1. Lấy g = 9,8m/s2. Quãng đường bóng đi được là :
Chọn chiều dương là chiều chuyển động của quả bóng.
Bóng chuyển động chậm dần đều dưới tác dụng của lực ma sát nên theo định luât II Niuton ta có:
\(\overrightarrow {{F_{ms}}} = m\overrightarrow a \,\,\,\left( * \right)\)
Chiếu (*) lên phương chuyển động ta có:
\(\begin{array}{l}{F_{ms}} = ma \Leftrightarrow - \mu N = ma \Leftrightarrow - \mu mg = ma\\ \Rightarrow a = - \mu g = - 0,1.9,8 = - 0,98m/{s^2}\end{array}\)
Áp dụng công thức liên hệ giữa s, v và a ta có:
\({v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{{0^2} - {{10}^2}}}{{2.\left( { - 0,98} \right)}} = 51m\)
Một cái thùng có khối lượng 50 kg trượt theo phương ngang trên sàn nhà dưới tác dụng của lực kéo không đổi có phương nằm ngang và có độ lớn 150 N. Biết hệ số ma sát trượt giữa thùng và mặt sàn là 0,2. Cho gia tốc rơi tự do g = 10m/s2. Gia tốc của thùng bằng.
Vì vật trượt trên phương ngang, và lực kéo theo phương ngang. Ta có :
\(\left\{ \begin{array}{l}
N = P\\
{F_{ms}} = \mu .N\\
F-{F_{ms}} = m.a
\end{array} \right.{\rm{ }} \Rightarrow F - \mu .N = F-\mu .m.g = m.a \Leftrightarrow 150-0,2.50.10 = 50.a \Leftrightarrow \;a = 1{\rm{ }}m/{s^2}\)
