Một vật được ném ngang từ độ cao $h$ so với mặt đất ở nơi có gia tốc rơi tự do $g$. Thời gian chạm đất của vật là:
Thời gian vật chạm đất: \(t = \sqrt {\dfrac{{2h}}{g}} \)
Ở nơi có gia tốc rơi tự gio là $g$, từ độ cao $h$ so với mặt đất, một vật được ném ngang với tốc độ ban đầu $v$. Tầm bay của vật là:
Tầm xa: \(L = v\sqrt {\dfrac{{2h}}{g}} \)
Quỹ đạo của chuyển động ném ngang là:
Phương trình quỹ đạo của vật ném ngang: \(y = \dfrac{g}{{2v_0^2}}{x^2}\)
=> quỹ đạo của chuyển động ném ngang là một đường parabol
Viên bi A khối lượng gấp đôi viên bi B. Cùng lúc, từ mái nhà, bi A được thả rơi không vận tốc đầu, bi B được ném theo phương ngang. Bỏ qua sức cản của không khí. Kết luận nào sau đây đúng?
Ta có:
+ Vật rơi tự do: \(h = \frac{1}{2}g{t^2} \to t = \sqrt {\frac{{2h}}{g}} \)
+ Thời gian vật ném ngang chạm đất: \(t = \sqrt {\frac{{2h}}{g}} \)
Ta thấy hai khoảng thời gian trên bằng nhau
=> Hai viên bi chạm đất cùng lúc
Một vật được ném ngang ở độ cao \(45{\rm{ }}m\) so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Thời gian vật rơi tới khi chạm đất là:
Ta có, thời gian chạm đất của vật ném ngang: \(t = \sqrt {\frac{{2h}}{g}} \)
Thay số, ta được: \(t = \sqrt {\frac{{2.45}}{{10}}} = 3{\rm{s}}\)
Một viên bi được ném theo phương ngang với vận tốc \(2{\rm{ }}m/s\) từ độ cao \(5{\rm{ }}m\) so với mặt đất. Lấy \(g = 10{\rm{ }}m/{s^2}\). Tầm ném xa của viên bi là:
Ta có, tầm xa của vật ném ngang: \(L = {v_0}\sqrt {\frac{{2h}}{g}} = 2\sqrt {\frac{{2.5}}{{10}}} = 2m\)
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao h so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều vận tốc đầu, Oy hướng thẳng đứng xuống dưới. Gốc thời gian là lúc ném. Lấy \(g = 10m/{s^2}\). Phương trình quỹ đạo của vật là:
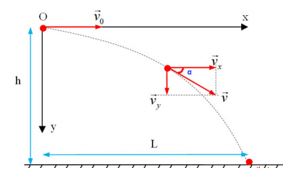
Phương trình chuyển động:
+ Theo phương Ox: \(x = {v_0}t\) (1)
+ Theo phương Oy: \(y = \dfrac{1}{2}g{t^2}\) (2)
Phương trình quỹ đạo (thay t ở (1) vào (2)): \(y = \dfrac{g}{{2v_0^2}}{x^2}\)
=> phương trình quỹ đạo của vật ném ngang trong trường hợp trên: \(y = \dfrac{g}{{2v_0^2}}{x^2} = \dfrac{{10}}{{{{2.10}^2}}} = 0,05{{\rm{x}}^2}\)
Một viên bi lăn theo cạnh của một mặt bàn nằm ngang cao \(1,25{\rm{ }}m\). Khi ra khỏi mép bàn nó rơi xuống nền nhà, cách mép bàn theo phương ngang \(2{\rm{ }}m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tốc độ của viên bi khi nó ở mép bàn là:
Ta có, tầm xa của vật: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \)
Vận tốc của vật khi ở mép bàn chính là vận tốc ban đầu:
\( \to {v_0} = \frac{L}{{\sqrt {\frac{{2h}}{g}} }} = \frac{2}{{\sqrt {\frac{{2.1,25}}{{10}}} }} = 4m/s\)
Một vật được ném ngang từ độ cao \(45{\rm{ }}m\) so với mặt đất ở nơi cố gia tốc rơi tự do \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \(40{\rm{ }}m/s\). Tốc độ của vật khi chạm đất là:
+ Thời gian chạm đất: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.45}}{{10}}} = 3{\rm{s}}\)
+ Vận tốc của vật theo các phương:
- Theo phương Ox: \({v_x} = {v_0} = 40\left( {m/s} \right)\)
- Theo phương Oy: \({v_y} = gt = 10.3 = 30\left( {m/s} \right)\)
Vận tốc của vật khi chạm đất: \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {{{40}^2} + {{30}^2}} = 50m/s\)
Ném vật theo phương ngang với vận tốc 10 m/s từ độ cao 40 m xuống đất. Lấy g = 10 m/s2. Phương trình quỹ đạo của vật và toạ độ của vật sau 2s là:
Ta có: \(g = 10m/{s^2};{\rm{ }}h = 40{\rm{ }}m;{\rm{ }}{v_0}\; = 10{\rm{ }}m/s\)
+ Phương trình quỹ đạo: \(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \dfrac{{10}}{{{{2.10}^2}}}.{x^2} = \dfrac{{{x^2}}}{{20}}\,\,\left( m \right)\)
+ Toạ độ của vật sau 2s là: \(\left\{ \begin{array}{l}x = {v_0}t = 10.2 = 20m\\y = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}{.10.2^2} = 20m\end{array} \right.\)
Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao 180cm. Khi ra khỏi mép, nó rơi xuống nền nhà tại điểm cách mép bàn 90cm (theo phương ngang). Lấy \(g = 10m/{s^2}\). Tính vận tốc của bi lúc rời khỏi bàn và viết phương trình quỹ đạo của viên bi.
Ta có: \(\left\{ \begin{array}{l}h = 180cm = 1,8m\\L = 90cm = 0,9m\\g = 10m/{s^2}\end{array} \right.\)
Chuyển động của hòn bi khi rời khỏi mặt bàn coi như là chuyển động ném ngang với độ cao ban đầu \(h = 1,8m\) và có tầm ném xa là \(L = 0,9m\).
Áp dụng công thức tính tầm ném xa ta có:
\(L = {v_0}.\sqrt {\dfrac{{2h}}{g}} \Rightarrow {v_0} = \dfrac{L}{{\sqrt {\dfrac{{2h}}{g}} }} = \dfrac{{0,9}}{{\sqrt {\dfrac{{2.1,8}}{{10}}} }} = 1,5m/s\)
Phương trình quỹ đạo của viên bi:
\(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \left( {\dfrac{{10}}{{2.1,{5^2}}}} \right).{x^2} = \dfrac{{20}}{9}{x^2}\,\left( m \right)\)
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao \(h\) so với mặt đất. Chọn hệ trục toạ độ \(Oxy\) sao cho gốc O trùng với vị trí ném, Ox theo chiều \(\overrightarrow {{v_0}} \), Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc bắt đầu ném. Phương trình quỹ đạo của vật là: (với \(g = 10m/{s^2}\) )
Ta có: \(\left\{ \begin{array}{l}{v_0} = 10m/s\\g = 10m/{s^2}\end{array} \right.\)
\( \Rightarrow \) Phương trình quỹ đạo của vật:
\(y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \left( {\dfrac{{10}}{{{{2.10}^2}}}} \right).{x^2} = 0,05.{x^2}\)
