Bài tập các lực trong thực tiễn

Lực hấp dẫn giữa hai vật (coi như chất điểm) tỉ lệ thuận với tích của hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

Lực ma sát nghỉ \(({\overrightarrow F _{m{\rm{s}}n}})\) chỉ xuất hiện khi có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.

Khi tốc độ của vật tăng thì hệ số ma sát giữa vật và mặt phẳng luôn không đổi

Ta có:

- Trái Đất: \(\left\{ \begin{array}{l}M\\R\end{array} \right.\)

- Mặt Trăng có khối lượng: \(M' = \frac{M}{{81}}\)

Gọi h là điểm mà tại đó lực hấp dẫn của Mặt Trăng tới điểm đó cân bằng với lực hấp dẫn của Trái Đất tới điểm đó.

=> Khoảng cách từ điểm đó tới Mặt Trăng là: \(60{\rm{R}} - h\)

Áp dụng biểu thức tính lực hấp dẫn, ta có:

+ Lực hấp dẫn do Trái Đất tác dụng lên điểm đó: \({F_{T{\rm{D}}}} = G\frac{{Mm}}{{{h^2}}}\)

+ Lực hấp dẫn do Mặt Trăng tác dụng lên điểm đó: \({F_{MT}} = G\frac{{Mm}}{{81{{\left( {60{\rm{R}} - h} \right)}^2}}}\)

Ta có:

\(\begin{array}{l}{F_{T{\rm{D}}}} = {F_{MT}} \leftrightarrow G\frac{{Mm}}{{{h^2}}} = G\frac{{Mm}}{{81{{\left( {60{\rm{R}} - h} \right)}^2}}}\\ \leftrightarrow 81{\left( {60{\rm{R}} - h} \right)^2} = {h^2}\\ \to 9(60{\rm{R}} - h) = h\\ \to h = 54{\rm{R}}\end{array}\)

Từ đầu bài, ta có:

\(\left\{ \begin{array}{l}{M_{SH}} = 0,1{M_{T{\rm{D}}}}\\{R_{SH}} = 0,53{{\rm{R}}_{TD}}\end{array} \right.\)  và gia tốc trọng trường trên mặt đất \(g = 9,8m/{s^2}\)

Áp dụng biểu thức tính gia tốc trọng trường ta có:

+ Gia tốc trọng trường trên mặt đất: \(g = G\frac{M_{T{\rm{D}}}}{{R_{T{\rm{D}}}^2}}{\rm{        }}\left( 1 \right)\)

+ Gia tốc trọng trường trên sao Hỏa: \({g_{SH}} = G\frac{{{M_{SH}}}}{{R_{SH}^2}}{\rm{        }}\left( 2 \right)\)

Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được:

\(\begin{array}{l}\frac{g}{{{g_{SH}}}} = \frac{{{M_{T{\rm{D}}}}R_{SH}^2}}{{{M_{SH}}R_{T{\rm{D}}}^2}} = \frac{{{M_{T{\rm{D}}}}.0,{{53}^2}R_{T{\rm{D}}}^2}}{{0,1{M_{T{\rm{D}}}}.R_{T{\rm{D}}}^2}} = 2,809\\ \to {g_{SH}} = \frac{g}{{2,809}} = \frac{{9,8}}{{2,809}} = 3,49m/{s^2}\end{array}\)

- Khi xe trượt trên đường ray, có 3 lực tác dụng lên xe:

+ Trọng lực: \(\overrightarrow P \)

+ Lực của đường ray: \(\overrightarrow Q \)

+ Lực ma sát trượt: \({\overrightarrow F _{_{mst}}}\)

- Theo định luật II Niutơn:

\(\overrightarrow P  + \overrightarrow Q  + {\overrightarrow F _{_{mst}}} = m\overrightarrow a \)

Mà: \(\overrightarrow P  + \overrightarrow Q  = \overrightarrow 0 \)

Nên: \({\overrightarrow F _{_{mst}}} = m\overrightarrow a \) (*)

- Chọn chiều dương là chiều chuyển động của xe.

\( - {F_{mst}} = ma\)

\( \Leftrightarrow  - {\mu _t}mg = ma\)

\( \Rightarrow a =  - {\mu _t}g =  - 0,2.9,8 =  - 1,96{\rm{ m/}}{{\rm{s}}^2}\)

- Quãng đường xe đi thêm được:

\({v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{0^2} - {{10}^2}}}{{2.( - 1,96)}} = 25,51{\rm{ m}}\)

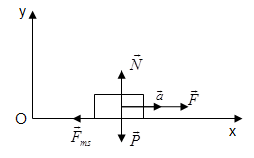
- Các lực tác dụng lên vật: Lực kéo \(\vec F\), lực ma sát \({\vec F_{ms}}\), trọng lực \(\vec P\), phản lực \(\vec N\)

- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.

- Phương trình định luật II Niu-tơn dưới dạng véc tơ:

\(\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\overrightarrow a \)       (1)

- Chiếu (1) lên trục Ox, Oy ta được:

\(\left\{ \begin{array}{l}F-{F_{ms}} = ma\\ - P + N = 0\;\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{F-{F_{ms}}}}{m}\\P = N\end{array} \right.\)

Có: \({F_{ms}} = {\mu _t}.N = {\mu _t}.P = {\mu _t}.mg\)

→ Gia tốc chuyển động của vật: \(a = \dfrac{{F - {F_{ms}}}}{m} = \dfrac{{F - {\mu _t}.mg}}{m}\)