Câu hỏi:
1 năm trước
Một vật nhỏ khối lượng m chuyển động theo trục Ox (trên một mặt ngang), dưới tác dụng của lực \(\vec F\) nằm ngang có độ lớn không đổi. Xác định gia tốc chuyển động của vật khi hệ số ma sát trượt trên mặt ngang bằng µt ?
Trả lời bởi giáo viên
Đáp án đúng: c
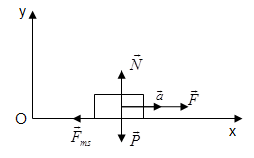
- Các lực tác dụng lên vật: Lực kéo \(\vec F\), lực ma sát \({\vec F_{ms}}\), trọng lực \(\vec P\), phản lực \(\vec N\)
- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\overrightarrow a \) (1)
- Chiếu (1) lên trục Ox, Oy ta được:
\(\left\{ \begin{array}{l}F-{F_{ms}} = ma\\ - P + N = 0\;\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{F-{F_{ms}}}}{m}\\P = N\end{array} \right.\)
Có: \({F_{ms}} = {\mu _t}.N = {\mu _t}.P = {\mu _t}.mg\)
→ Gia tốc chuyển động của vật: \(a = \dfrac{{F - {F_{ms}}}}{m} = \dfrac{{F - {\mu _t}.mg}}{m}\)
Hướng dẫn giải:
Phương pháp động lực học:
Bước 1: Chọn vật (hệ vật) khảo sát.
Bước 2: Chọn hệ quy chiếu (Cụ thể hoá bằng hệ trục toạ độ vuông góc; Trục toạ độ Ox luôn trùng với phương chiều chuyển động; Trục toạ độ Oy vuông góc với phương chuyển động)
Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ.
Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niu Tơn.
\(\overrightarrow {{F_{hl}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = m.\overrightarrow a \) (*) (Tổng tất cả các lực tác dụng lên vật)
Bước 5: Chiếu phương trình lực (*) lên các trục toạ độ Ox, Oy:
Ox: F1x + F2x + … + Fnx = ma (1)
Oy: F1y + F2y + … + Fny = 0 (2)
Giải phương trình (1) và (2) ta thu được đại lượng cần tìm
Câu hỏi khác
- Bài tập trắc nghiệm Ba định luật Newton về chuyển động môn Vật lí lớp 10 sách CTST có lời giải
- Bài tập bài tập lực - tổng hợp lực - ba định luật newton lí 10 có lời giải
- Bài tập trắc nghiệm Một số lực trong thực tiễn môn Vật lí lớp 10 sách CTST có lời giải
- Bài tập bài tập các lực trong thực tiễn lí 10 có lời giải
- Bài tập trắc nghiệm Chuyển động của vật trong chất lưu môn Vật lí lớp 10 sách CTST có lời giải
