Chuyển động thẳng đều là:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
Chọn phát biểu đúng?
Độ dời không phụ thuộc vào hình dạng của quỹ đạo chuyển động mà chỉ phụ thuộc vào vị trí điểm đầu và vị trí điểm cuối
Véctơ vận tốc trung bình của vật được xác định bởi biểu thức:
Véctơ vận tốc trung bình của vật được xác định bởi biểu thức: →vtb=Δ→xΔt
Chọn phát biểu sai: Chuyển động thẳng đều là chuyển động của chất điểm trên một đường thẳng và:
A - sai vì : Chuyển động thẳng đều có vận tốc không đổi: v=const
B, C, D - đúng
Từ thực tế, hãy xem trường hợp nào dưới đây, quỹ đạo chuyển động của vật là một đường thẳng?
A- quỹ đạo của hòn đá có dạng cong
B- đường từ Hà Nội - TP. HCM có nhiều khúc quanh co, ngoằn nghèo => quỹ đạo của xe oto không phải là đường thẳng
C- quỹ đạo của viên bi là một đường thẳng
D- quỹ đạo của tờ giấy là đường cong, ngoằn nghèo
Chọn phương án sai?
A, C, D - đúng
B- sai vì: Vận tốc trung bình là đại lượng vật lý có hướng cùng hướng với độ dời Δ→x được xác định trong khoảng thời gian Δt
Chọn gốc tọa độ không trùng với vị trí ban đầu, gốc thời gian trùng với thời điểm ban đầu thì phương trình chuyển động của chất điểm chuyển động thẳng đều có dạng:
Do: Chọn gốc tọa độ không trùng với vị trí ban đầu, gốc thời gian trùng với thời điểm ban đầu
=> phương trình chuyển động của chất điểm: x=x0+vt
Phương trình vận tốc của chuyển động thẳng đều:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Hay nói cách khác, vận tốc của chuyển động không đổi: v=const
Một thang máy mang một người từ tầng trệt đi xuống tầng hầm sâu 5m, rồi lên đến tầng 3 . Biết rằng mỗi tầng cách nhau 4m. Trục toạ độ có gốc và chiều dương như hình vẽ. Quãng đường chuyển động khi người này lên đến tầng 3?
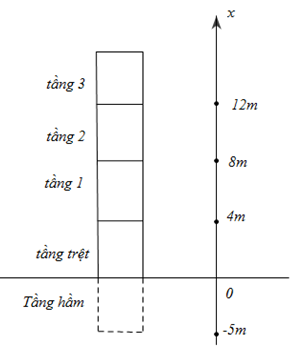
Ta có: Thang máy di chuyển từ tầng trệt - tầng hầm - tầng trệt - tầng 1 - tầng 2 - tầng 3:
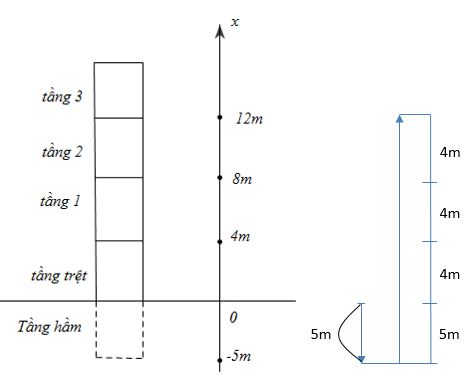
=> Quãng đường chuyển động khi người này lên đến tầng 3 là:
S=5.2+4+4+4=22m
Đồ thị tọa độ - thời gian trong chuyển động thẳng của chất điểm có dạng như hình vẽ. Trong khoảng thời gian nào chất điểm chuyển động thẳng đều?
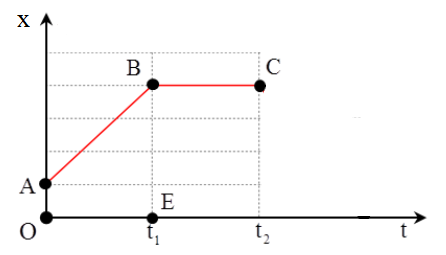
Từ đồ thị ta có:
+ Từ 0 đến t1: vật chuyển động thẳng đều
+ Từ t1 đến t2: vật đứng yên
Một người chạy bộ theo đường thẳng AB = 50m, từ A đến B rồi quay về A. Gốc toạ độ O ở trong khoảng AB, cách A một khoảng 10m, chiều dường từ A đến B.
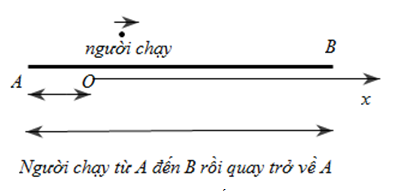
Độ dời từ A khi người này đến O là:
Ta có:
Toạ độ điểm A là
xA=¯OA=−10m , toạ độ điểm B là xB=40m
Độ dời khi đến O: s1=xO−xA=0−(−10)=10(m)
Bạn Việt đi xe đạp đến trường theo đường thẳng như hình vẽ. Khi đến quán báo, bạn sực nhớ đã quên một cuốn sách ở nhà nên quay về nhà lấy sách rồi lại đạp xe đến trường.

Độ dời khi bạn quay từ quán báo về nhà và độ dời khi bạn từ quán báo đến trường lần lượt là:
Ta có:
Độ dời khi bạn Việt từ quán báo về nhà:
s2=¯BO=−¯OB=−xB=−400m
Độ dời khi bạn Việt từ quán báo đến trường:
s3=¯BT=¯OT−¯OB=xT−xB=1000m−400m=600m
Hình sau cho biết đồ thị tọa độ của một chiếc xe chuyền động trên đường thẳng. Vận tốc của xe là:
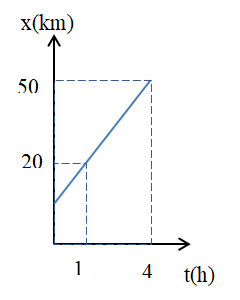
Theo đồ thị: lúc t1 = 1 h, x1 = 20 km; lúc t2 = 4 h, x2 = 50 km
→v=x2−x1t2−t1=50−204−1=10(km/h)
Trong một lần thử xe ô tô, người ta xác định được vị trí của xe tại các thời điểm cách nhau cùng khoảng thời gian 1s (xem bảng dưới đây). Vận tốc trung bình của ô tô trong 3 giây cuối cùng là:
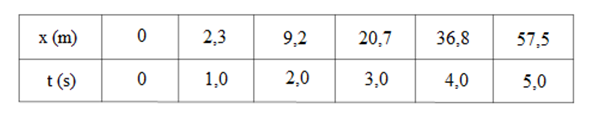
Ta có: Vận tốc trung bình: vtb=ΔxΔt
Trong 3s cuối, oto có:
+ Độ dời: Δx=57,5−9,2=48,3m
+ Khoảng thời gian: Δt=3s
→vtb=ΔxΔt=48,33=16,1(m/s)
Một người tập thể dục chạy trên một đường thẳng. Lúc đầu người đó chạy với vận tốc trung bình 5m/s trong thời gian 4 phút. Sau đó người ấy giảm vận tốc còn 4m/s trong thời gian 3 phút. Người đó chạy được trên quãng đường bằng bao nhiêu?
Ta có:
+ Quãng đường chạy trong 4 phút đầu là: s1=5.(4.60)=1200m
+ Quãng đường chạy trong 3 phút sau là: s2=4.(3.60)=720m
Quãng đường người đó chạy được là: s=s1+s2=1200+720=1920m=1,920km
Chất điểm chuyển động trên đường thẳng, vật xuất phát từ gốc tọa độ chuyển động theo chiều dương, tại các thời điểm khác nhau vật có vị trí tọa độ như bảng dưới:

Phương trình chuyển động của vật là:
Ta có:
+ Chất điểm chuyển động trên đường thẳng, vật xuất phát từ gốc tọa độ chuyển động theo chiều dương
+ Vận tốc: v=Δx1Δt1=2,5−01−0=2,5(m/s)
+ Tại thời điểm ban đầu: t0=0;x0=0
=> Phương trình chuyển động của vật: x=x0+vt=2,5t
Một chiếc xe chạy trên đoạn đường 40km với tốc độ trung bình là 80km/h, trên đoạn đường 40km tiếp theo với tốc độ trung bình là 40km/h. Tốc độ trung bình của xe trên đoạn đường 80km này là:
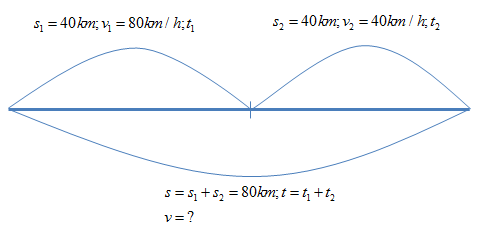
Ta có:
+ Thời gian chuyển động trên đoạn s1 là: t1=s1v1=4080=0,5h
+ Thời gian chuyển động trên đoạn s2 là: t2=s2v2=4040=1h
→ Thời gian chuyển động trên đoạn đường s=80km:
t=t1+t2=0,5+1=1,5h
⇒ Tốc độ trung bình vtb=st=801,5≈53,3km/h.
Một chiếc xe từ A đến B mất một khoảng thời gian t với tốc độ trung bình là 48km/h. Trong 1/4 khoảng thời gian đầu nó chạy với tốc độ trung bình là v1=30km/h. Trong khoảng thời gian còn lại nó chạy với tốc độ trung bình bằng:
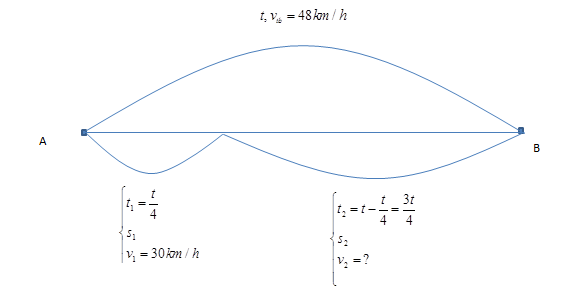
Quãng đường xe chạy từ A đến B: s=48t
Quãng đường xe chạy trong t4: s1=v1t1=30t4=7,5t
Quãng đường xe chạy trong thời gian còn lại t2=t−t4=3t4 là: s2=s−s1=48t−7,5t
Tốc độ trung bình trong khoảng thời gian còn lại là: v2=s2t2=48t−7,5t0,75t=54km/h
Một ôtô chuyển động từ A về B. Chặng đầu xe đi mất 15 tổng thời gian với vận tốc v1. Chặng giữa xe đi mất 14 tổng thời gian với vận tốc v2 = 60km/h. Chặng còn lại xe chuyển động với vận tốc v3 = 40km/h. Biết vận tốc của xe trên cả quãng đường AB là v = 47 km/h. Tính v1.
Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.
Thời gian xe đi hết chặng cuối là: t−t5−t4=1120t
Độ dài quãng đường AB là: S=v.t=47t (1)
Theo bài ta có:
S=v1.t5+v2.t4+v3.11t20=v1.t5+60.t4+4011t20=v1.t5+37t(2)
⇒47.t=v1.t5+37t⇒v1=50km/h
Một ôtô chuyển động từ A về B. Chặng đầu xe đi mất 13 tổng thời gian với vận tốc v1 = 45km/h. Chặng giữa xe đi mất 12 tổng thời gian với vận tốc v2 = 60km/h. Chặng còn lại xe chuyển động với vận tốc v3 = 48km/h. Tính vận tốc của xe trên cả quãng đường AB.
Gọi t là tổng thời gian xe chuyển động từ A về B, v là vận tốc trung bình của xe.
Thời gian xe đi hết chặng cuối là: t−t3−t2=t6
Độ dài quãng đường AB là: S=v.t (1)
Theo bài ta có: S=v1.t3+v2.t2+v3.t6=45.t3+60.t2+48t6=53t(2)
Từ (1) và (2) suy ra: v.t=53t⇒v=53km/h

