Chọn phương án đúng,
A, D - sai vì: Quỹ đạo và vận tốc của chuyển động có tính tương đối
B - sai vì: Vận tốc trong các hệ quy chiếu khác nhau là khác nhau
C - đúng
Trạng thái đứng yên hay chuyển động có tính tương đối vì trạng thái chuyển động
Trạng thái đứng yên hay chuyển động có tính tương đối vì trạng thái chuyển động được quan sát trong nhiều hệ quy chiếu khác nhau.
Một hành khách ngồi trên toa tàu A, nhìn qua cửa sổ thấy toa tàu B bên cạnh và gạch lát sân ga đều chuyển động như nhau. Nếu lấy vật mốc là nhà ga thì:
Khi hành khách ngồi trên toa tàu A, mà thấy toa tàu B bên cạnh và gạch lát sân ga đều chuyển động như nhau => véctơ vận tốc có phương, chiều và độ lớn như nhau
Mặt khác, gạch lát sân ga đứng yên => Tàu B cũng đứng yên
=> Tàu A chuyển động
Vậy, Tàu A chuyển động, tàu B đứng yên
Nhận xét nào sau đây của hành khách ngồi trên đoàn tàu đang chạy là không đúng?
A, C, D - đúng
B - sai vì: Khi hành khách ngồi trên đoàn tàu đang chạy sẽ thấy đầu tàu đứng yên so với toa tàu
Đứng ở Trái Đất ta sẽ thấy:
Khi đứng ở Trái Đất, ta sẽ thấy
+ Trái Đất đứng yên
+ Mặt Trăng và Mặt Trời quay quanh Trái Đất
Biểu thức nào sau đây là biểu thức đúng của công thức cộng vận tốc:
Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Trong đó:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tuyệt đối.
Khẳng định nào sau đây là đúng. Từ công thức vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \), ta kết luận:
Từ công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \), ta suy ra
A - sai vì: nếu \(\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} \) thì \({v_{13}} = {v_{12}} + {v_{23}}\)
B - sai vì: nếu \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \) cùng phương thì \({v_{13}} = {v_{12}} \pm {v_{23}}\) tùy theo chiều của hai vận tốc
C - sai vì: \(\overrightarrow {{v_{13}}} \) có chiều phụ thuộc vào chiều và độ lớn của cả hai vận tốc
D - đúng
Một chiếc thuyền đi trong nước yên lặng với vận tốc có độ lớn \({v_1}\), vận tốc dòng chảy của nước so với bờ sông có độ lớn \({v_2}\). Nếu người lái thuyền hướng mũi thuyền dọc theo dòng nước từ hạ nguồn lên thượng nguồn của con sông thì một người đứng trên bờ sẽ thấy:
+ \({v_{12}} = {v_1}\): vận tốc của thuyền so với dòng
+ \({v_{23}} = {v_2}\): vận tốc của dòng so với bờ
+ \({v_{13}}\): vận tốc của thuyền so với bờ
Áp dụng công thứ cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Ta suy ra: khi \({v_1} > {v_2}\) => thuyền chuyển động về phía thượng nguồn
Muốn một vật từ một máy bay đang bay trên trời rơi thẳng đứng xuống mặt đất thì
Muốn một vật từ một máy bay đang bay trên trời rơi thẳng đứng xuống mặt đất thì ta ném vật ngược chiều bay với vận tốc bằng vận tốc máy bay.
Một chiếc thuyền chuyển động trên đoạn đường \(AB\) dài \(60km\). Vận tốc của thuyền là \(15km/h\) so với dòng nước yên lặng. Tính vận tốc dòng chảy của nước biết thời gian để thuyền đi từ \(A\) đến \(B\) rồi quay lại \(A\) là \(9\) tiếng?
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}} = 15km/h\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
- Khi thuyền đi xuôi dòng: \({v_{13}} = {v_{12}} + {v_{23}}\)
Khi thuyền đi ngược dòng: \(v{'_{13}} = {v_{12}} - {v_{23}}\)
- Gọi \({t_1},{t_2}\) lần lượt là thời gian đi và về của thuyền, ta có:
\(\left\{ \begin{array}{l}{t_1} = \frac{{AB}}{{{v_{13}}}} = \frac{{AB}}{{{v_{12}} + {v_{23}}}}\\{t_2} = \frac{{AB}}{{v{'_{13}}}} = \frac{{AB}}{{{v_{12}} - {v_{23}}}}\end{array} \right.\)
Theo đầu bài, ta có:
\(\begin{array}{l}{t_1} + {t_2} = 9 \to \frac{{AB}}{{{v_{12}} + {v_{23}}}} + \frac{{AB}}{{{v_{12}} - {v_{23}}}} = 9\\ \leftrightarrow \frac{{60}}{{15 + {v_{23}}}} + \frac{{60}}{{15 - {v_{23}}}} = 9\\ \leftrightarrow 60\left( {15 - {v_{23}}} \right) + 60\left( {15 + {v_{23}}} \right) = 9\left( {{{15}^2} - v_{23}^2} \right)\\ \to {v_{23}} = 5km/h\end{array}\)
Một chiếc thuyền chạy ngược dòng nước từ \(A\) đến \(B\) mất \(6\) giờ, xuôi dòng mất \(3\) giờ. Nếu tắt máy để thuyền tự trôi theo dòng nước thì đi từ bến \(A\) đến bến \(B\) mất mấy giờ?
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}}\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
Thuyền tắt máy trôi theo dòng tương đương thuyền chuyển động với vận tốc \({v_{23}}\)
- Khi thuyền ngược dòng: \({v_{13}} = {v_{12}} - {v_{23}}\)
Khi xuôi dòng: \(v{'_{13}} = {v_{12}} + {v_{23}}\)
- Gọi \({t_1},{t_2}\) lần lượt là thời gian đi ngược dòng và đi xuôi dòng của thuyền, ta có:
\(\left\{ \begin{array}{l}{v_{13}} = \frac{{AB}}{{{t_1}}} = \frac{{AB}}{6}{\rm{ }}\left( 1 \right)\\v{'_{13}} = \frac{{AB}}{{{t_2}}} = \frac{{AB}}{3}{\rm{ }}\left( 2 \right)\end{array} \right.\)
Lấy \(\left( 1 \right) - \left( 2 \right) = 2{v_{23}} = \frac{{AB}}{6} \to {v_{23}} = \frac{{AB}}{{12}}\)
=> Nếu tắt máy để thuyền tự trôi theo dòng nước thì đi từ bến \(A\) đến bến \(B\) mất thời gian: \(t = \frac{{AB}}{{{v_{23}}}} = \frac{{AB}}{{\frac{{AB}}{{12}}}} = 12\) giờ
Một chiếc thuyền xuôi dòng từ \(A\) đến \(B\), vận tốc của dòng nước \(5km/h\). Chiều dài từ \(A\) đến \(B\) là bao nhiêu? Biết thuyền xuôi dòng mất \(2\) giờ và ngược dòng mất \(3\) giờ trên cùng đoạn đường AB
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}}\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
- Khi xuôi dòng: \(v{'_{13}} = {v_{12}} + {v_{23}}\)
Khi thuyền ngược dòng: \({v_{13}} = {v_{12}} - {v_{23}}\)
- Gọi \({t_1},{t_2}\) lần lượt là thời gian đi xuôi dòng và đi ngược dòng của thuyền, ta có:
\(\left\{ \begin{array}{l}{t_1} = \frac{{AB}}{{{v_{13}}}} = \frac{{AB}}{{{v_{12}} + {v_{23}}}} = 2{\rm{ }}\left( 1 \right)\\{t_2} = \frac{{AB}}{{v{'_{13}}}} = \frac{{AB}}{{{v_{12}} - {v_{23}}}} = 3{\rm{ }}\left( 2 \right)\end{array} \right.\)
Từ (1) và (2), ta suy ra:
\(\begin{array}{l}2{v_{12}} + 2{v_{23}} = 3{v_{12}} - 3{v_{23}}\\ \to {v_{12}} = 5{v_{23}} = 5.5 = 25km/h\end{array}\)
Thế vào (1), ta được: \(AB = 2\left( {{v_{12}} + {v_{23}}} \right) = 2\left( {25 + 5} \right) = 60km\)
Trên một tuyến đường xe bus BRT, các xe bus chuyển động theo một chiều và cách đều nhau \(5km\). Một người đi xe đạp chuyển động thẳng đều trên tuyến đường này. Nếu đi theo một chiều thì tại thời điểm \(t = 0\), người đi xe đạp gặp xe bus thứ nhất, đến thời điểm \(t = 1h\) người này gặp xe bus thứ \(12\). Nếu đi theo chiều ngược lại thì thời điểm \(t = 0\), người đi xe đạp gặp xe bus thứ nhất, đến thời điểm \(t = 1h\) người này gặp xe bus thứ \(6\). Nếu người này đứng yên bên đường thì trong \(1h\) tính từ thời điểm gặp xe bus thứ nhất, người này còn gặp được bao nhiêu xe bus nữa? Bỏ qua kích thước của xe bus và xe đạp.
Ta có:
+ Người đi xe đạp (1)
+ Xe bus (2)
+ Đường (3)
+ Vận tốc của người đi xe đạp (1) so với xe bus (2): \({v_{12}}\)
+ Vận tốc của xe bus (2) so với đường (3): \({v_{23}}\)
+ Vận tốc của người đi xe đạp (1) so với đường (2): \({v_{13}}\)
Theo đề bài, ta có:
Sau \(1h\) gặp xe bus số \(12\) => Xe đạp chuyển động ngược chiều xe bus
Sau \(1h\) gặp xe bus số \(6\) => Xe đạp chuyển động cùng chiều xe bus
Xe đạp chuyển động ngược chiều với xe bus:
\(\begin{array}{l}{v_{13}} = {v_{23}} - {v_{12}}\\ \to {v_{12}} = {v_{23}} + {v_{13}} = \frac{S}{t} = \frac{{11.5}}{1} = 55km/h{\rm{ }}\left( 1 \right)\end{array}\)
Người đi xe đạp chuyển động cùng chiều với đoàn xe bus:
\(\begin{array}{l}{v_{13}} = {v_{23}} + {v_{12}}\\ \to {v_{12}} = {v_{23}} - {v_{13}} = \frac{S}{t} = \frac{{5.5}}{1} = 25km/h{\rm{ }}\left( 2 \right)\end{array}\)
Từ (1) và (2), ta suy ra: \({v_{23}} = 40km/h\)
=> Nếu người đó đứng yên thì số xe bus đi qua là: \(\frac{{40}}{5} = 8\)
Một chiếc thuyền chuyển động từ điểm $A$ của bờ này đến điểm $B$ của bờ kia của con sông, do nước chảy xiết thuyền không đến được bờ $B$ mà gần đến điểm $C$ cách bờ $180m$. Xác định vận tốc của thuyền so với dòng nước? Biết sông rộng $240m$, thời gian qua sông là $1$ phút
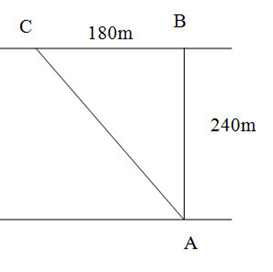
Ta có:
+ Thuyền (1)
+ Dòng nước (2)
+ Bờ sông (3)
+ Vận tốc của thuyền (1) so với dòng nước (2): \({v_{12}}\)
+ Vận tốc của dòng nước (2) so với bờ (3): \({v_{23}}\)
+ Vận tốc của thuyền (1) so với bờ (2): \({v_{13}}\)
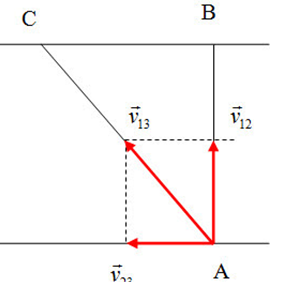
Thời gian qua sông là $1$ phút:
\(\left\{ \begin{array}{l}{v_{13}} = \dfrac{{AC}}{t} = \dfrac{{\sqrt {A{B^2} + B{C^2}} }}{{60}} = 5m/s\\{v_{12}} = {v_{13}}.c{\rm{os}}\alpha = {v_{13}}\dfrac{{AB}}{{AC}} = 4m/s\end{array} \right.\)
Vậy vận tốc của thuyền so với dòng là: \({v_{12}} = 4m/s\)
Một thang cuốn tự động đưa khách từ tầng $1$ lên tầng $2$ mất $1,4$ phút. Nếu không dùng thang người đi bộ phải mất khoảng thời gian là $4,6$ phút để đi từ tầng $1$ lên tầng $2$. Coi vận tốc của người đi bộ và thang cuốn là không đổi. Nếu thang cuốn vẫn chuyển động và người đó vẫn bước đi trên thang cuốn thì thời gian từ tầng $1$ lên tầng $2$ là bao nhiêu?
Gọi s là quãng đường từ tầng 1 lên tầng 2
Ta có:
+ Người (1)
+ Thang cuốn (2)
+ Mặt đất (3)
+ Vận tốc của người đi bộ so với thang cuốn đứng yên: \({v_{12}} = \dfrac{s}{{4,6}}\)
+ Vận tốc của thang cuốn so với đất: \({v_{23}} = \dfrac{s}{{1,4}}\)
Người bước lên thang cuốn chuyển động
=> Người chuyển động cùng chiều với thang cuốn
Áp dụng công thức cộng vận tốc, ta có:
\(\begin{array}{l}{v_{13}} = {v_{12}} + {v_{23}}\\ \leftrightarrow \dfrac{s}{t} = \dfrac{s}{{4,6}} + \dfrac{s}{{1,4}}\\ \to t = 1,073 \approx 1,07\end{array}\)
Một chiếc xe đang chạy với vận tốc \(18km/h\) trong mưa, giả sử mưa rơi thẳng đứng và đều đối với mặt đất. Người ngồi trên xe thấy các giọt mưa tạo một góc \({30^0}\) so với phương thẳng đứng. Vận tốc rơi của hạt mưa đối với đất có giá trị là:
Ta có:
+ Hạt mưa (1)
+ Xe (2)
+ Mặt đất (3)
+ \({v_{12}}\): vận tốc của hạt mưa so với xe
+ \({v_{23}} = 18km/h\): vận tốc của xe so với mặt đất
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên
- Vận dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Theo đầu bài ta có:
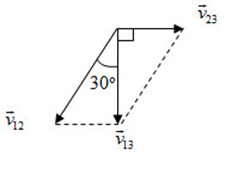
Từ hình, ta suy ra:
\(\begin{array}{l}\tan {30^0} = \frac{{{v_{23}}}}{{{v_{13}}}}\\ \to {v_{13}} = \frac{{{v_{23}}}}{{\tan {{30}^0}}}\\ = \frac{{18}}{{\frac{1}{{\sqrt 3 }}}} = 18\sqrt 3 km/h = 5\sqrt 3 m/s \approx 8,66m/s\end{array}\)
Một chiếc thuyền chạy ngược dòng trên một đoạn sông thẳng, sau 1 giờ đi được 9km so với bờ. Một đám củi khô trôi trên sông đó, sau 1 phút trôi được 50m so với bờ. Vận tốc của thuyền so với nước là:
Ta có: \(\left\{ \begin{array}{l}{v_{tb}} = \dfrac{{{s_1}}}{{{t_1}}} = \dfrac{9}{1} = 9km/h\\{v_{nb}} = \dfrac{{{s_2}}}{{{t_2}}} = \dfrac{{50}}{{60}} = \dfrac{5}{6}m/s = 3km/h\end{array} \right.\)
Ta có: \(\overrightarrow {{v_{tb}}} = \overrightarrow {{v_{tn}}} + \overrightarrow {{v_{nb}}} \)
Do thuyền chạy ngược dòng sông nên:
\({v_{tb}} = {v_{tn}} - {v_{nb}} \Rightarrow {v_{tn}} = {v_{tb}} + {v_{nb}} = 9 + 3 = 12km/h\)
Một tàu thủy chở hàng đi xuôi dòng sông trong 4 giờ đi được 100 km, khi chạy ngược dòng trong 4 giờ thì đi được 60 km. Tính vận tốc của tàu so với nước. Coi vận tốc của nước đối bờ là luôn luôn không đổi.
Vật (1): Tàu thuỷ; Vật (2): dòng nước; Vật (3): bờ sông.
Với \(\overrightarrow {{v_{12}}} \,\)là vận tốc của tàu so với nước; \(\,\,\overrightarrow {{v_{23}}} \) là vận tốc của nước so với bờ.
Thời gian chuyển động là: \(t = \dfrac{{AB}}{{{v_{13}}}}\)
+ Tàu đi xuôi dòng ta có \(\overrightarrow {{v_{12}}} \, \uparrow \uparrow \,\,\overrightarrow {{v_{23}}} \)
Vận tốc của tàu so với bờ là: \({v_{13}} = {v_{12}} + {v_{23}}\)
mà \({v_{13}} = \dfrac{{{S_1}}}{{{t_x}}} = \dfrac{{100}}{4} = 25km/h \Rightarrow {v_{12}} + {v_{23}} = 25\,\,\left( {km/h} \right)\,\,\,\left( * \right)\)
+ Tàu đi ngược dòng ta có: \(\overrightarrow {{v_{12}}} \, \uparrow \downarrow \,\,\overrightarrow {{v_{23}}} \)
Vận tốc của tàu so với bờ là: \({v_{13}}' = {v_{12}} - {v_{23}}\)
mà \({v_{13}}' = \dfrac{{{S_2}}}{{{t_x}}} = \dfrac{{60}}{4} = 15km/h \Rightarrow {v_{12}} - {v_{23}} = 15\,\,\left( {km/h} \right)\,\,\,\left( {**} \right)\)
Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}{v_{12}} + {v_{23}} = 25\\{v_{12}} - {v_{23}} = 15\end{array} \right.\, \Rightarrow \left\{ \begin{array}{l}{v_{12}} = 20km/h\\{v_{23}} = 5km/h\end{array} \right.\)
→ Vận tốc của tàu so với nước là v12 = 20 km/h
Một canô xuôi dòng từ bến A đến bến B mất 4 giờ, còn nếu đi ngược dòng từ bến B đến bến A hết 9 giờ. Biết dòng nước chảy với tốc độ 10 km/h. Độ lớn vận tốc của canô so với dòng nước là bao nhiêu?
Vật (1): cano; Vật (2): dòng nước; Vật (3): bờ sông.
Thời gian cano đi từ bến A đến bến B là: \(t = \dfrac{{AB}}{{{v_{13}}}}\)
+ Cano đi xuôi dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow \uparrow \,\,\overrightarrow {{v_{23}}} \)
→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}} = {v_{12}} + {v_{23}} = {v_{12}} + 10\,\,\left( {km/h} \right)\)
Thời gian đi xuôi dòng là: \({t_x} = \dfrac{{AB}}{{{v_{12}} + 5}} = 4\,\,\left( h \right)\,\,\,\,\,\,\,\,\left( * \right)\)
+ Cano đi ngược dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow \downarrow \,\,\overrightarrow {{v_{23}}} \,\,\,\left( {{v_{12}} > {v_{23}}} \right)\)
→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}}' = {v_{12}} - {v_{23}} = {v_{12}} - 10\,\,\left( {km/h} \right)\)
Thời gian đi ngược dòng là: \({t_n} = \dfrac{{AB}}{{{v_{12}} - 5}} = 9\,\,\left( h \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {**} \right)\)
Từ (1) và (2) ta có: \(\dfrac{{\left( * \right)}}{{\left( {**} \right)}} \Leftrightarrow \dfrac{{{v_{12}} - 10}}{{{v_{12}} + 10}} = \dfrac{4}{9} \Rightarrow {v_{12}} = 26\,\left( {km/h} \right)\)
A ngồi trên một toa tàu chuyển động với vận tốc 15 km/h đang rời ga. B ngồi trên một toa tàu khác chuyển động với vận tốc 10 km/h đang vào ga. Hai đường tàu song song với nhau. Tính vận tốc của B đối với A. Chọn chiều dương là chiều chuyển động của tàu A.
Chọn chiều dương là chiều chuyển động của tàu A
Gọi: + \(\overrightarrow {{v_{BD}}} \) vận tốc của tàu B đối với đất, \(\overrightarrow {{v_{BD}}} \) ngược chiều dương nên vBD = -10 km/h
+ \(\overrightarrow {{v_{AD}}} \) vận tốc của tàu A đối với đất, \(\overrightarrow {{v_{AD}}} \)theo chiều dương nên vAD = 15 km/h
+ \(\overrightarrow {{v_{BA}}} \) vận tốc của tàu B đối với tàu A
Theo công thức cộng vận tốc: \(\overrightarrow {{v_{BA}}} = \overrightarrow {{v_{BD}}} + \overrightarrow {{v_{DA}}} = \overrightarrow {{v_{BD}}} - \overrightarrow {{v_{AD}}} \)
\( \Rightarrow {v_{BA}} = {v_{BD}} - {v_{AD}} = - 10 - 15 = - 25\,km/h\)
Chứng tỏ vận tốc của tàu B so với tàu A có độ lớn 25km/h và ngược chiều so với chiều chuyển động của tàu A
