Câu hỏi:
1 năm trước
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:
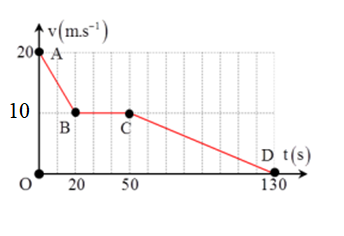
Quãng đường mà ôtô đi được là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
+ Trên đoạn \(A \to B\) xe chuyển động chậm dần đều với gia tốc: \({a_1} = \frac{{{v_B} - {v_A}}}{{\Delta t}} = \frac{{10 - 20}}{{20}} = - 0,5m/{s^2}\)
Quãng đường vật đi được: \({s_1} = 20t - 0,25{t^2} = 20.20 - 0,{25.20^2} = 300m\)
+ Trên đoạn \(B \to C\) xe chuyển động thẳng đều với vận tốc \(v = 10m/s\)
Quãng đường vật đi được: \({s_2} = vt = 10.30 = 300m\)
+ Trên đoạn \(C \to D\) xe chuyển động chậm dần đều với gia tốc:
\({a_3} = \frac{{0 - 10}}{{130 - 50}} = - 0,125m/s{}^2\)
Quãng đường vật đi được: \({s_3} = 10t - 0,0625{t^2} = 10.80 - 0,{0625.80^2} = 400m\)
Vậy quãng đường mà ôtô đi được là: \(s = {s_1} + {s_2} + {s_3} = 300 + 300 + 400 = 1000m\)
Hướng dẫn giải:
+ Đọc đồ thị v - t
+ Vận dụng biểu thức: \(s = v.t\)
Câu hỏi khác
- Bài tập trắc nghiệm Gia tốc – Chuyển động thẳng biến đổi đều môn Vật lí lớp 10 sách CTST có lời giải
- Bài tập sự rơi tự do. gia tốc rơi tự do lí 10 có lời giải
- Bài tập bài tập chuyển động thẳng biến đổi đều lí 10 có lời giải
- Bài tập bài tập sự rơi tự do lí 10 có lời giải
- Bài tập trắc nghiệm Chuyển động ném môn Vật lí lớp 10 sách CTST có lời giải
