Dưới tác dụng của lực \(\overrightarrow F \) như hình. Thanh AB có thể quay quanh điểm A. Cánh tay đòn của lực \(\overrightarrow F \) trong trường hợp này bằng bao nhiêu? Biết \(AB = 5cm\).
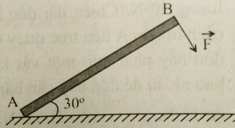
Cánh tay đòn của lực F là:
\(d = AB = 5cm\)
Tính momen của lực \(\overrightarrow F \) đối với trục quay O, cho biết \(F = 100N\), \(OA = 100cm\). Bỏ qua trọng lượng của thanh.
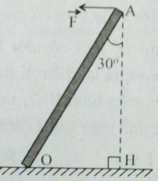
Ta có:
\(d = AH = OA.\cos {30^0} = 100.\dfrac{{\sqrt 3 }}{2} = 50\sqrt 3 \left( {cm} \right)\)
Suy ra: momen của lực:
\(M = F.d = 100.0,5\sqrt 3 = 50\sqrt 3 N.m\)
Một thanh đồng chất có trọng lượng \(P\) được gắn vào tường nhờ một bản lề và được giữ nằm ngang bằng một dây treo thẳng đứng như hình. Xét momen lực đối với bản lề. Hãy chọn câu đúng.
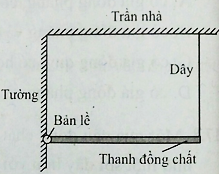
Thanh cân bằng => theo quy tắc momen, ta có: \({M_T} = {M_P}\) hay momen của lực căng bằng momen của trọng lực
Một thanh dài \(L\), trọng lượng \(P\), được treo nằm ngang vào tường như hình.
Một vật có trọng lượng \({P_1}\) được treo ở đầu thanh. Dây treo làm với thanh một góc \(\alpha \). Lực căng của dây bằng
Thanh cân bằng => theo quy tắc momen, ta có: \({M_T} = {M_P}\) hay momen của lực căng bằng momen của trọng lực
\( \to T\sin \alpha = \dfrac{1}{2}P + {P_1}\)
hay \(T = \dfrac{{\dfrac{1}{2}P + {P_1}}}{{\sin \alpha }}\)
Một bàn đạp có trọng lượng không đáng kể, có chiều dài \(OA = 20cm\), quay dễ dàng quanh trục O nằm ngang như hình. Một lò xo gắn vào điểm giữa C. Người ta tác dụng lên bàn đạp tại điểm A một lực \(\overrightarrow F \) vuông góc với bàn đạp và có độ lớn \(20N\). Bàn đạp ở trạng thái cân bằng khi lò xo có phương vuông góc với OA và bị ngắn đi một đoạn \(8cm\) so với khi không bị nén. Lực của lò xo tác dụng lên bàn đạp và độ cứng của lò xo là:
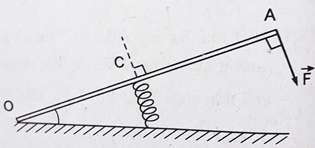
Ta có, thanh cân bằng, áp dụng quy tắc momen, ta có:
\(\begin{array}{l}{F_{dh}}.OC = F.OA\\ \Rightarrow {F_{dh}} = \dfrac{{F.OA}}{{OC}} = \dfrac{{20.0,2}}{{0,1}} = 40N\end{array}\)
\(\begin{array}{l}{F_{dh}} = k\Delta l\\ \Rightarrow k = \dfrac{{{F_{dh}}}}{{\Delta l}} = \dfrac{{40}}{{0,08}} = 500N/m\end{array}\)
Một thanh cứng AB dài \(7m\), có khối lượng không đáng kể, có trục quay O, hai đầu chịu 2 lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) như hình. Cho \({F_1} = 50N\); \({F_2} = 200N\) và \(OA = 2m\) . Đặt vào thanh một lực \({F_3}\) hướng lên và có độ lớn \(300N\) để cho thanh nằm ngang. Khoảng cách OC là
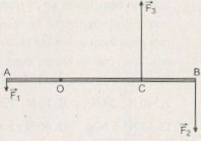
Ta có:
AO = 2m, AB = 7m
\({F_1} = 50N,{F_2} = 200N,{F_3} = 300N\)
+ Thanh cân bằng và tâm quay tại O, theo quy tắc momen, ta có:\({M_A} = {M_B} - {M_C}\)(1)
+ \(\left\{ \begin{array}{l}{M_A} = {F_1}.AO\\{M_C} = {F_3}.OC\\{M_B} = {F_2}.OB\end{array} \right.\)
thay vào (1) ta được:
\(\begin{array}{l}{F_1}.AO = {F_2}.OB - {F_3}.OC\\ \to OC = \dfrac{{{F_2}.OB - {F_1}.OC}}{{{F_3}}} = \dfrac{{5.200 - 50.2}}{{300}} = 3m\end{array}\)
Một người nâng một tấm gỗ nặng \(30kg\) dài \(1,5m\), lực nâng vuông góc với tấm gỗ và giữ cho nó hợp với mặt đất nằm ngang một góc \(\alpha = {30^0}\). Biết trọng tâm của tấm gỗ cách đầu mà người đó nâng \(120cm\). Tính lực nâng của người đó.
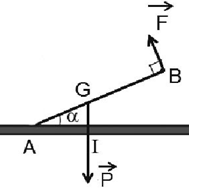
Ta có:
m = 30kg, AB = 1,5m, GB = 1,2m
Tâm quay tại A
Cánh tay đòn của lực F:\(AB\)
Cánh tay đòn của lực P: \(AI = AG.c{\rm{os}}\alpha \)
+ Theo quy tắc momen, ta có: \({M_P} = {M_F}\)(1)
+ \(\left\{ \begin{array}{l}{M_P} = P.AI = P.AG.c{\rm{os}}\alpha \\{M_F} = F.AB\end{array} \right.\) (2)
Từ (1) và (2), ta suy ra:
\(\begin{array}{l}P.AG.c{\rm{os}}\alpha = F.AB\\ \leftrightarrow mg.AG.c{\rm{os30}} = F.AB\\ \to F = \dfrac{{mg.AG.c{\rm{os30}}}}{{AB}} = \dfrac{{30.10.(1,5 - 1,2).c{\rm{os30}}}}{{1,5}} = 30\sqrt 3 N\end{array}\)
Một thanh BC nhẹ, gắn vào tường bởi bản lề C, đầu B treo vật có khối lượng \(m = 4kg\) và được giữ cân bằng nhờ dây treo \(AB\). Cho \(AB = 30cm,AC = 40cm\). Xác định lực tác dụng lên BC
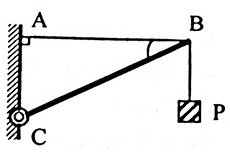
+ Áp dụng quy tăc momen lực với trục quay qua B, ta có:
\({M_P} = {M_T}\)
+ Mặt khác:\(\left\{ \begin{array}{l}{M_F} = P.AB\\{M_T} = T.AB.\sin \alpha \end{array} \right.\)
ta suy ra:
\(\begin{array}{l}P.AB = T.AB.sin{30^0}\\ \to T = \dfrac{F}{{\sin {\alpha ^0}}} = \dfrac{{40}}{{\dfrac{4}{5}}} = 50N\end{array}\)
Một thanh gỗ nặng \(12kg\) dài \(1,5m\), một đầu được gắn cố định đi qua điểm A, thanh gỗ có thể quay xung quanh trục đi qua A, đầu còn lại được buộc vào một sợi dây sao cho phương của sợi dây thẳng đứng và giữ cho tấm gỗ nằm nghiêng hợp với phương ngang một góc \(\alpha \). Biết trọng tâm của thanh gỗ cách đầu \(A\) khoảng \(50cm\). Tính lực căng của sợi dây? Lấy \(g = 10m/{s^2}\)
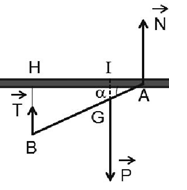
+ Áp dụng quy tắc momen, ta có:\({M_T} = {M_P}\)
+ Mặt khác: \(\left\{ \begin{array}{l}{M_T} = T.AB.c{\rm{os}}\alpha \\{M_P} = P.AG.c{\rm{os}}\alpha \end{array} \right.\)
Ta suy ra:
\(\begin{array}{l}T.AB.c{\rm{os}}\alpha {\rm{ = P}}{\rm{.AG}}{\rm{.cos}}\alpha \\ \to {\rm{T}}{\rm{.AB = P}}{\rm{.}}\dfrac{{AB}}{3} \to T = \dfrac{P}{3} = \dfrac{{120}}{3} = 40N\end{array}\)
Một cái thước AB đặt trên mặt bàn nhẵn nằm ngang, có trục quay O cách đầu A một khoảng \(80cm\). Một lực \({F_1} = 10N\) tác dụng lên đầu A theo phương vuông góc với thước và lực thứ hai \(\overrightarrow {{F_2}} \) tác dụng lên điểm C của thước và theo phương vuông góc với thước (không vẽ trên hình) và cách A \(30cm\). Các lực đều nằm trên mặt phẳng nằm ngang. Nếu thước không chuyển động thì lực \(\overrightarrow {{F_2}} \) có hướng và độ lớn
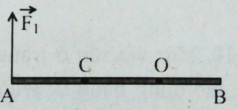
Ta có, 2 lực ở hai bên so với trục quay
Thước không chuyển động, nên:
+ Áp dụng quy tắc momen, ta có: \({M_{{F_1}}} = {M_{{F_2}}}\)
+ Mặt khác: \(\left\{ \begin{array}{l}{M_{{F_1}}} = {F_1}.AO\\{M_{{F_2}}} = {F_2}.CO\end{array} \right.\)
Ta suy ra:
\(\begin{array}{l}{F_1}.AO = {F_2}.CO\\ \to {F_2} = \dfrac{{{F_1}.AO}}{{CO}} = \dfrac{{10.0,8}}{{0,5}} = 16N\end{array}\)
Và \(\overrightarrow {{F_2}} \uparrow \downarrow \overrightarrow {{F_1}} \)
Dùng cân đòn để cân một vật. Vì cánh tay đòn của cân không thật bằng nhau nên khi đặt vật ở đĩa cân bên này ta được 25g nhưng khi đặt vật sang bên kia ta cân được 31,36g. Khối lượng đúng của vật là:
Gọi “đĩa cân bên này” là đĩa cân 1, “đĩa cân bên kia” là đĩa cân 2; \({P_x}\) là trọng lượng của vật cần cân.
Áp dụng quy tắc momen, ta có:
Khi cân lần 1: \({P_1}{l_1} = {P_x}{l_2} \to {m_1}{l_1} = {m_x}{l_2}\) (1)
Khi cân lần 2: \({P_x}{l_1} = {P_2}{l_2} \to {m_x}{l_1} = {m_2}{l_2}\) (2)
Lấy (1) chia cho (2), ta được:
\(\dfrac{{{m_1}}}{{{m_x}}} = \dfrac{{{m_x}}}{{{m_2}}} \to {m_x} = \sqrt {{m_1}{m_2}} = \sqrt {25.31,36} = 28g\)
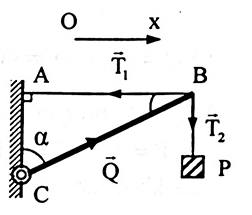
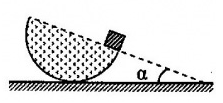
Bán cầu đồng chất khối lượng \(150g\). Trên mép bán cầu đặt một vật nhỏ khối lượng \(6,5g\). Hỏi mặt phẳng của bán cầu sẽ nghiêng góc \(\alpha \) bao nhiêu khi có cân bằng. Biết rằng trọng tâm bán cầu ở cách mặt phẳng của bán cầu một đoạn \(\dfrac{{3R}}{8}\) (R - bán kính bán cầu)
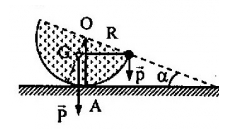
+ Các lực tác dụng lên bán cầu gồm: trọng lực \(\overrightarrow P \) (bán cầu), trọng lực \(\overrightarrow p \) (vật nhỏ), phản lực \(\overrightarrow Q \) (tại điểm tiếp xúc A)
+ Áp dụng quy tắc momen lực đối với trục quay qua O, ta có:
\({M_P} = {M_p}\) (vì \(\overrightarrow Q \) có giá đi qua trục quay tại A nên \({M_Q} = 0\))
+ Mặt khác, ta có: \(\left\{ \begin{array}{l}{M_P} = P.OG.\sin \alpha \\{M_p} = p.R.c{\rm{os}}\alpha \end{array} \right.\)
=> Ta suy ra:
\(\begin{array}{l}P.OG.\sin \alpha = p.R.c{\rm{os}}\alpha \\ \leftrightarrow Mg.\dfrac{{3R}}{8}\sin \alpha = mgRc{\rm{os}}\alpha \\ \to {\rm{M}}\dfrac{3}{8}\sin \alpha = mc{\rm{os}}\alpha \\ \to {\rm{tan}}\alpha {\rm{ = }}\dfrac{{8m}}{{3M}} = \dfrac{{8.6,5}}{{3.150}} = 0,12\\ \to \alpha = {7^0}\end{array}\)
Đòn bẩy AB dài 50 cm nhẹ, cứng như hình vẽ
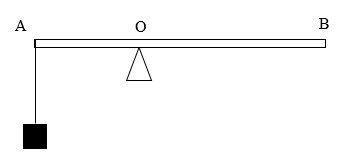
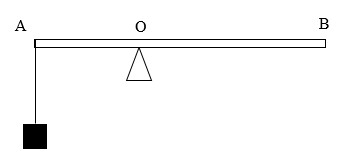
Đầu A của đòn bẩy treo một vật có trọng lượng 30N. Khoảng cách từ đầu A đến trục quay O là 20 cm. Muốn đòn bẩy AB cân bằng thì đầu B của đòn bẩy phải treo vật có trọng lượng là
Trọng lượng của vật cần treo vào đầu B có trọng lượng là PB
Theo quy tắc momen ta có M1 = M2 ó PA.dA = PB.dB ó 30.20 = PB.30
=> PB = 20 N
Momen của một lực đối với một trục quay là đại lượng đặc trưng cho?
Xét một lực \(\overrightarrow F \) nằm trong mặt phẳng vuông góc với trục quay Oz.
Momen của lực \(\overrightarrow F \) đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực quanh trục ấy và được đo bằng tích độ lớn của lực với cánh tay đòn.
Mômen lực được xác định bằng công thức:
Xét một lực \(\overrightarrow F \) nằm trong mặt phẳng vuông góc với trục quay Oz. Momen của lực \(\overrightarrow F \) đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực quanh trục ấy và được đo bằng tích độ lớn của lực với cánh tay đòn.
\(M = F{\rm{d}}\)
Momen lực có đơn vị là:
\(M = F{\rm{d}}\)
=> Momen lực có đơn vị là: N.m
Đoạn thẳng nào sau đây là cánh tay đòn của lực?
d (cánh tay đòn): là khoảng cách từ trục quay tới giá của lực
Nhận xét nào sau đây là đúng. Quy tắc mômen lực:
Quy tắc momen lực dùng được cho cả vật rắn có trục quay cố định và không có trục quay cố định nếu như trong một tình huống cụ thể nào đó ở vật xuất hiện trục quay.
Để có mômen của một vật có trục quay cố định là 10 Nm thì cần phải tác dụng vào vật một lực bằng bao nhiêu? Biết khoảng cách từ giá của lực đến tâm quay là 20cm.
Ta có, momen của lực: \(M = F{\rm{d}}\)
theo yêu cầu của đề bài, ta suy ra:
\(F = \dfrac{M}{d} = \dfrac{{10}}{{0,2}} = 50N\)
Mômen lực của một lực đối với trục quay là bao nhiêu nếu độ lớn của lực là 5,5 N và cánh tay đòn là 2 mét ?
Ta có, momen của lực: \(M = Fd = 5,5.2 = 11N.m\)

