Định luật 2 Newton

Chọn chiều dương là chiều chuyển động của vật

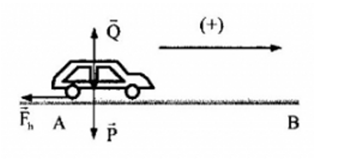
+ Các lực tác dụng lên vật: trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \), lực hãm \(\overrightarrow {{F_h}} \)

+ Phương trình định luật II Niutơn cho vật: \(\overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_h}}  = m\overrightarrow a \) (1)

Chiếu (1) lên chiều dương, ta được: \( - {F_h} = ma\) (2)

+ Mặt khác, ta có phương trình vận tốc: \(v = {v_0} + at\)

khi xe dừng lại \(v = 0 \to {v_0} =  - at\) (3)

Khi đó, quãng đường đi được của xe: \(s = {v_o}t + \frac{1}{2}a{t^2} =  - a{t^2} + \frac{1}{2}a{t^2} =  - \frac{1}{2}a{t^2}\) (4)

Từ (4), ta suy ra: \(a = \frac{{ - 2{\rm{s}}}}{{{t^2}}} = \frac{{ - 2.9}}{{{3^2}}} =  - 2m/{s^2}\)

=> thay vào (2), ta có: Lực hãm \({F_h} =  - ma =  - 2000.( - 2) = 4000N\)  

Định luật II - Niutơn: Véctơ gia tốc của một vật luôn cùng hướng với lực tác dụng lên vật. Độ lớn của véctơ gia tốc tỉ lệ thuận với độ lớn của véctơ lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật.

\(\overrightarrow a  = \dfrac{{\overrightarrow F }}{m}\) hay \(\overrightarrow F  = m\overrightarrow a \)

+ Độ lớn lực kéo của động cơ của:

• Xe 1 là: \({F_1} = {m_1}{a_1}\)
• Xe 2 là: \({F_2} = {m_2}{a_2}\)

+ Chọn trục tọa độ Ox trùng vời đường thẳng AB, gốc O trùng với A, mốc thời gian là lúc hai xe khởi hành

+ Phương trình chuyển động của hai xe:

• Xe 1: \({x_1} = 5t + \frac{1}{2}{a_1}{t^2}\)
• Xe 2: \({x_2} = 30 + \frac{1}{2}{a_2}{t^2}\)

Ta có, khoảng cách giữa hai xe:

\(\Delta x = {x_2} - {x_1} = 30 + \frac{1}{2}{a_2}{t^2} - \left( {5t + \frac{1}{2}{a_1}{t^2}} \right)\)

Theo đầu bài, ta có: \({a_2} = 2{{\rm{a}}_1}\)

\( \to \Delta x = 30 + {a_1}{t^2} - \left( {5t + \frac{1}{2}{a_1}{t^2}} \right) = \frac{1}{2}{a_1}{t^2} - 5t + 30\) (*)

Tam thức (*) có hệ số lớn hơn 0, ta suy ra: \(\Delta {x_{\min }} = \frac{{ - \Delta }}{{4{\rm{a}}}} = \frac{{ - (25 - 60{{\rm{a}}_1})}}{{2{{\rm{a}}_1}}}\)

Mặt khác, theo đầu bài:

\(\begin{array}{l}\Delta {x_{\min }} = 5m \leftrightarrow \frac{{ - (25 - 60{{\rm{a}}_1})}}{{2{{\rm{a}}_1}}} = 5\\ \to {a_1} = 0,5m/{s^2}\end{array}\)

=> Lực kéo của mỗi động cơ xe là:

\(\left\{ \begin{array}{l}{F_1} = {m_1}{a_1} = 1000.0,5 = 500N\\{F_2} = {m_2}{a_2} = 1000.2.0,5 = 1000N\end{array} \right.\)

Khối lượng của vật là đại lượng đặc trưng cho mức quán tính của vật.

Ta có:

+ Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.

+ Định luật II Niutơn: \(\overrightarrow F  = m\overrightarrow a \)

=> Khi vật chịu tác dụng của một lực duy nhất thì nó sẽ bị biến dạng hoặc biến đổi vận tốc (do gia tốc đặc trưng cho sự biến đổi vận tốc của vật)

Chọn chiều dương trùng chiều chuyển động của xe

Lực hãm xe có độ lớn \(F\)

+ Theo định luật II Niutơn, ta có gia tốc của các xe:

\({a_A} = \dfrac{{ - F}}{{{m_A}}};{a_B} = \dfrac{{ - F}}{{{m_B}}}\) (1)

(do các xe chuyển động chậm dần đều, lực hãm có chiều ngược chiều chuyển động)

+ Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\)

=> Quãng đường xe A và xe B đi được thêm là:

\({s_A} =  - \dfrac{{v_0^2}}{{2{a_A}}};{s_B} =  - \dfrac{{v_0^2}}{{2{a_B}}}\) (2)

Theo đầu bài, ta có:

\(\begin{array}{*{20}{l}}{{s_B} < {s_A} \leftrightarrow  - \dfrac{{v_0^2}}{{2{a_B}}} <  - \dfrac{{v_0^2}}{{2{a_A}}}}\\{ \leftrightarrow \dfrac{{v_0^2}}{{2{a_B}}} > \dfrac{{v_0^2}}{{2{a_A}}} \to {a_A} > {a_B}}\end{array}\)

Kết hợp với (1), ta được:

\(\begin{array}{l} \to \dfrac{{ - F}}{{{m_A}}} > \dfrac{{ - F}}{{{m_B}}}\\ \leftrightarrow \dfrac{1}{{{m_A}}} < \dfrac{1}{{{m_B}}}\\ \to {m_B} < {m_A}\end{array}\)

Ta có:  \(v = 54km/h = 15m/s\)

+ Chọn chiều (+)  là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.

Theo định luật II - Niutơn, ta có: \(\overrightarrow a  = \frac{{\overrightarrow F }}{m} \to a =  - \frac{F}{m} =  - \frac{{3000}}{{1000}} =  - 3m/{s^2}\)  

+ Mặt khác, ta có:

\(\begin{array}{l}{v^2} - v_0^2 = 2{\rm{as}} \leftrightarrow 0 - {15^2} = 2.( - 3)s\\ \to {\rm{s}} = {\rm{37,5m}}\end{array}\)

+ Theo định luật II Niutơn, ta có: \(a = \frac{F}{m} = 750m/{s^2}\)

+ Chọn gốc thời gian là lúc chân cầu thủ chạm vào bóng

+ Phương trình vận tốc của vật: \(v = {v_0} + at = 0 + 750.0,015 = 11,25\,m/s\)

Theo định luật II Niuton ta có độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực

\( \Rightarrow \) Khi độ lớn hợp lực tác dụng lên vật tăng lên nhưng không đổi hướng thì gia tốc của vật sẽ tăng lên.

Ta có:

+ Ban đầu: \({a_1} = \frac{{\Delta {v_1}}}{{\Delta t}} = \frac{2}{5} = 0,4m/{s^2}\)

Mặt khác, ta có: \({F_1} = m{a_1} = 0,4m\)

+ Khi tăng \(F' = 2.{F_1} = {\rm{2}}{\rm{.0,4m}} = 0,8m\)

\( \to {{\rm{a}}_2} = \frac{{0,8m}}{m} = 0,8m/{s^2}\)

Lại có: \({a_2} = \frac{{\Delta {v_2}}}{{\Delta t}} = \frac{{\Delta {v_2}}}{8} = 0,8m/{s^2} \to \Delta {v_2} = 6,4m/s\)

+ Ta có:

\({v^2} - v_0^2 = 2{\rm{as}} \to  - v_0^2 = 2{\rm{as}} = 3,6{\rm{a   }}(1)\)

Mặt khác: \(a = \dfrac{{v - {v_0}}}{{\Delta t}} \to  - {v_0} = at = 2a{\rm{          (2)}}\)

Từ (1) và (2) ta suy ra: \(a =  - 0,9{\rm{ }}m/{s^2}\)

+ Lực hãm phanh tác dụng lên ôtô: \(F = m.a{\rm{ }} =  - 450N\)

Theo định luật II Niutơn, ta có:

 \(\begin{array}{l}{m_1} = \frac{F}{{{a_1}}};{m_2} = \frac{F}{{{a_2}}}\\ \to {a_3} = \frac{F}{{{m_3}}} = \frac{F}{{{m_1} + {m_2}}} = \frac{F}{{\frac{F}{{{a_1}}} + \frac{F}{{{a_2}}}}}\\ = \frac{{{a_1}{a_2}}}{{{a_1} + {a_2}}} = \frac{{2.3}}{{2 + 3}} = 1,2m/{s^2}\end{array}\)

Theo định luật II - Niutơn, ta có: \(F = ma\)

+ Khi \(m = {m_1} = 4kg\) thì \({a_1} = 3m/{s^2}\)

+ Khi \(m = {m_2}\) thì \({a_2} = 2m/{s^2}\)

Ta có, lực trong hai trường hợp là như nhau:

\(\begin{array}{l} \leftrightarrow {m_1}{a_1} = {m_2}{a_2} \leftrightarrow 4.3 = {m_2}.2\\ \to {m_2} = 6kg\end{array}\)

=> Khối lượng vật thêm vào là: \(6 - 4 = 2kg\)  

Gọi m và m’ lần lượt là khối lượng của xe và của kiện hàng.

Chọn chiều dương là chiều chuyển động của xe

+ Áp dụng định luật II Niutơn:

• cho xe: \({a_1} = \frac{F}{m}\) (1)
• cho xe và kiện hàng: \({a_2} = \frac{F}{{m + m'}}\) (2)

+ Quãng đường đi của xe trong hai trường hợp là: \(s = \frac{1}{2}{a_1}t_1^2 = \frac{1}{2}{a_2}t_2^2\) (3)

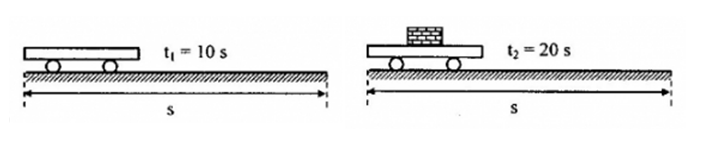
Từ (3), ta suy ra: \(\frac{{{a_1}}}{{{a_2}}} = \frac{{t_2^2}}{{t_1^2}} = \frac{{{{20}^2}}}{{{{10}^2}}} = 4\)

Từ (1) và (2), ta suy ra: \(\frac{{{a_1}}}{{{a_2}}} = \frac{{m + m'}}{m} \to m' = 3m = 3.50 = 150kg\)

+Áp dụng định luật II - Niutơn cho vật:

• Trên đoạn đường AB: \({a_1} = \frac{{{F_1}}}{m}\) (1)
• Trên đoạn đường BC: \({a_2} = \frac{{{F_2}}}{m}\) (2)

Lấy (2)/(1) ta được: \(\frac{{{a_2}}}{{{a_1}}} = \frac{{{F_2}}}{{{F_1}}}\) (3)

+ Mặt khác, ta có:

• \({a_1} = \frac{{{v_1} - {v_{01}}}}{t} = \frac{{10 - 0}}{t} = \frac{{10}}{t}\)
• \({a_2} = \frac{{{v_2} - {v_{02}}}}{t} = \frac{{15 - 10}}{t} = \frac{5}{t}\)

Thay vào (3), ta được: \(\frac{{{F_2}}}{{{F_1}}} = \frac{{\frac{5}{t}}}{{\frac{{10}}{t}}} = \frac{1}{2}\)

Ta có: \(S = {v_0}t + \dfrac{1}{2}a{t^2}\)

\(\begin{array}{l} \Leftrightarrow 30 = 2.3 + 0,5.a{.3^2}\\ \Rightarrow a = \dfrac{{16}}{3}m/{s^2}\end{array}\)

Lực cản của không khí tác dụng vào vật có độ lớn bằng:

\(\begin{array}{l}P - {F_C} = ma\\ \Rightarrow {F_c} = p - ma \\= mg - ma = 50 - 5.\dfrac{{16}}{3} = 23,33N\end{array}\)

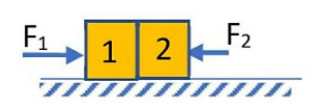
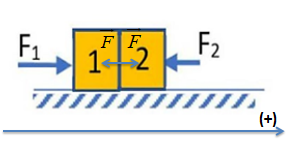
Chiếu các lực lên chiều dương, ta được:

\({F_1} - F = ma\) (1)

\(F - {F_2} = ma\) (2)

Lấy (1) – (2), ta được:

\({F_1} - F - F + {F_2} = 0 \Leftrightarrow 2F = {F_1} + {F_2}\)

\( \Leftrightarrow F = \frac{{{F_1} + {F_2}}}{2}\)