Bài tập về chuyển động thẳng - thẳng biến đổi điều

Chuyển động thẳng nhanh dần đều: a cùng dấu với v (véctơ gia tốc cùng phương cùng chiều với véctơ vận tốc)

Trong chuyển động thẳng biến đổi đều, quãng đường đi được trong những khoảng thời gian bằng nhau là không bằng nhau. Chỉ khi vật chuyển động thẳng đều thì quãng đường đó với nhau.

Trong chuyển động thẳng nhanh dần đều, véc tơ gia tốc của vật có hướng và độ lớn không đổi.

Trong chuyển động nhanh dần đều véctơ gia tốc của vật cùng chiều với véc tơ vận tốc

Ta có trong chuyển động biến đổi đều \(\vec a\) và \(\Delta \vec v\) luôn cùng chiều khi chất điểm chuyển động theo chiều dương

Vật sẽ chuyển động chậm dần nếu a và v trái dấu hay a < 0  và  v₀ > 0

sau 10s ta có vận tốc: \(v = 10 + 2.10 = 30(m/s)\)

Chọn mốc tại A

Ta có phương trình xe chuyển động từ A là: \({x_A} = {x_0} + {v_1}t = 30t\)

Phương trình xe chuyển động từ B là: \({x_B} = {x_0}' + {v_2}t = 150 - 20t\)

Khi hai xe gặp nhau ta có: \({x_A} = {x_B}\)

\(\begin{array}{l} \Leftrightarrow 30t = 150 - 20t\\ \Rightarrow t = 3h\end{array}\)

Ta có phương trình tọa độ: \(x = 25 + 30t\)

\( \Rightarrow v = 30\left( {m/s} \right)\)

Áp dụng công thức tính quãng đường ta có: \(s = v.t\)

sau 2h quãng đường chất điểm đi được là: \(s = 30.0,5.60.60 = 54000m = 54km\)

Tại thời điểm t=0,5s ta có tọa độ của chất điểm là: \(x{\rm{  = }}10 + 4.0,5 = 12\left( {m/s} \right)\)

Trong chuyển động chậm dần đều ta có a và v trái dấu nên \(v = 15 - 3t\) là phương trình của vật chuyển động chậm dần đều

- Chọn chiều dương là chiều chuyển động

ta có: \({v_0} = 54km/h = 15m/s\)

Khi xe dừng lại v = 0 ta có:

- Áp dụng công thức tính vận tốc: \( \Rightarrow a = \dfrac{{v - {v_0}}}{t} = \dfrac{{0 - 15}}{6} =  - 2,5\left( {m/{s^2}} \right)\)

Quãng đường ô tô đi được đến khi dừng là: \(s = {v_0}t + \dfrac{1}{2}a{t^2} = 15.6 + \dfrac{1}{2}\left( { - 2,5} \right){.6^2} = 45m\)

Chọn mốc tại A, chiều dương từ A đến B và mốc thời gian là 8h

Ta có:

phương trình chuyển động của xe thứ nhất là:

\(\begin{array}{l}{x_1} = {x_0} + {v_{01}}t + \dfrac{1}{2}{a_1}{t^2} = 10t - \dfrac{1}{2}.0,2.{t^2}\\ \Rightarrow {x_1} = 10t - 0,1.{t^2}\end{array}\)

phương trình chuyển động của xe thứ 2 là:

\(\begin{array}{l}{x_2} = {x_0} + {v_{02}}t + \dfrac{1}{2}{a_2}{t^2}\\ \Rightarrow {x_2} = 560 - 0,2{t^2}\end{array}\)

khi người đi xe đuổi kịp ta có: \({x_1} = {x_2}\)

\(\begin{array}{l} \Leftrightarrow 10t - 0,1{t^2} = 560 - 0,2.{t^2}\\ \Rightarrow t = 40(s)\end{array}\)

nơi gặp nhau cách A: \({x_1} = 10t - 0,1.{t^2} = 10.40 - 0,{1.40^2} = 240m\)

vậy hai xe gặp nhau lúc 8h40s tại nơi cách A 240m.

Đổi 54km/h=15m/s

Ta có công thức liên hệ: \({v^2} - v_0^2 = 2a{\rm{s}}\)

\(\begin{array}{l} \Leftrightarrow {0^2} - {15^2} = 2.a.150\\ \Rightarrow a =  - 0,75\left( {m/{s^2}} \right)\end{array}\)

Ta có trong chuyển động nhanh dần đều vận tốc v và gia tốc a cùng dấu

phương trình quãng đường là: \(s = {v_0}t + \dfrac{1}{2}a{t^2}\)

Áp dụng phương trình vận tốc: \(v = {v_0} + at\)

\( \Rightarrow a = \dfrac{{{v_1} - {v_0}}}{{{t_1}}} = \dfrac{{35 - 20}}{{25}} = 0,6m/{s^2}\)

Áp dụng phương trình vận tốc ta có vận tốc của xe sau 1 phút tăng ga là: \({v_2} = {v_0} + a{t_2} = 20 + 0,6.60 = 56m/s\)

Từ phương trình \({\rm{x}} = {\rm{4}}{{\rm{t}}^{\rm{2}}}{\rm{ + 8t}} + {\rm{6}}\) ta có: \({v_0} = 8(m/s);a = 2.4 = 8(m/{s^2})\)

Phương trình vận tốc của vật: \(v = {v_0} + at \Leftrightarrow v = 8 + 8t\)

Quãng đường vật chuyển động là: \(s = {v_0}t + \dfrac{1}{2}a{t^2}\)

\(\begin{array}{l} \Rightarrow 50 = \dfrac{1}{2}a{.10^2}\\ \Rightarrow a = 1\left( {m/{s^2}} \right)\end{array}\)

Quãng đường đi trong 4s cuối là: \(s = {s_{10}} - {s_6} = 50 - \dfrac{{{6^2}}}{2} = 32\left( m \right)\)

ta có sơ đồ minh họa quá trình chuyển động:

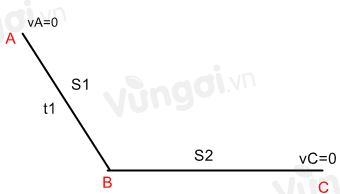
Gia tốc của quả cầu ở chân dốc B là:

\({a_1} = \dfrac{{2\left( {{s_1} - {v_A}{t_1}} \right)}}{{t_1^2}} = \dfrac{{2\left( {150 - 0} \right)}}{{{{15}^2}}} = \dfrac{4}{3}\left( {m/{s^2}} \right)\)

khi đó vận tốc của quả cầu khi ở B là: \({v_B} = {v_A} + {a_1}{t_1} = 0 + \dfrac{4}{3}.15 = 20\left( {m/s} \right)\)

Gia tốc của quả cầu khi chuyển động trên mặt ngang là: \({a^2} = \dfrac{{v_C^2 - v_B^2}}{{2{{\rm{s}}_2}}} = \dfrac{{{0^2} - {{20}^2}}}{{2.75}} = \dfrac{{ - 8}}{3}\left( {m/{s^2}} \right)\)

thời gian quả cầu chuyển động trên mặt ngang là: \({t_2} = \dfrac{{{v_C} - {v_B}}}{{{a_2}}} = \dfrac{{0 - 20}}{{ - \dfrac{8}{3}}} = 7,5{\rm{s}}\)

tổng thời gian chuyển động của quả cầu là: \(t = {t_1} + {t_2} = 15 + 7,5 = 22,5{\rm{s}}\)

Vận tốc trong chuyển động thẳng đều được xác định bằng công thức \(v = \dfrac{s}{t}\)