Một vật có khối lượng 1kg chuyển động với vận tốc 2m/s thì va chạm vào một vật có khối lượng 3kg đang đứng yên. Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc. Độ lớn vận tốc ngay sau va chạm đó là:
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của vật 1, vật 2 và của 2 vật sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{1.2 + 3.0}}{{1 + 3}} = 0,5\,m/s\)
Một người nặng 50kg đang chạy với vận tốc 3m/s thì nhảy lên một xe đẩy nặng 150kg đang chạy trên đường ngang song song với người với vận tốc 2m/s. Vận tốc của xe ngay sau khi người nhảy lên trong trường hợp xe chạy cùng chiều với người có độ lớn là:
Chọn chiều dương là chiều chuyển động của hai vật
Người và xe va chạm mềm. Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của người, xe lúc trước và của xe lúc sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{50.3 + 150.2}}{{50 + 150}} = 2,25\,m/s\)
Một người nặng 50kg đang chạy với vận tốc 3m/s thì nhảy lên một xe đẩy nặng 150kg đang chạy trên đường ngang song song với người với vận tốc 2m/s. Vận tốc của xe ngay sau khi người nhảy lên trong trường hợp xe chạy ngược chiều với người có độ lớn là:
Chọn chiều dương là chiều chuyển động của người
Người và xe va chạm mềm. Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của người, xe lúc trước và của xe lúc sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{50.3 - 150.2}}{{50 + 150}} = - 0,75\,m/s\)
Với v2 = -150 m/s vì xe chuyển động ngược chiều so với người
Vậy độ lớn của xe sau va chạm là 0,75 m/s
Một vật có khối lượng \(m\) chuyển động với vận tốc v1 đến va chạm với một vật có khối lượng \(2m\) đang đứng yên. Sau va chạm, hai vật dính vào nhau và cùng chuyển động với vận tốc là 1m/s. Tính vận tốc v1?
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của vật 1, vật 2 và của 2 vật sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} < = > 1 = \frac{{m.{v_1} + 2m.0}}{{m + 2m}} < = > {v_1} = 3\,m/s\)
Một người có khối lượng \(50\left( {kg} \right)\) đang chạy với tốc độ \(5\left( {m/s} \right)\) thì nhảy lên chiếc xe lăn có khối lượng \(150\left( {kg} \right)\) đang chuyển động cùng hướng. Nếu bỏ qua ma sát của xe trên mặt đường thì sau khi nhảy lên, người và xe có cùng tốc độ bằng \(1,625\left( {m/s} \right)\). Tính vận tốc của xe lăn trước va chạm?
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của người, xe trước và xe sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} < = > 1,625 = \dfrac{{50.5 + 150.{v_2}}}{{50 + 150}} < = > {v_2} = 0,5\,m/s\)
Một viên đạn đang bay theo phương ngang với vận tốc $600 m/s$ thì xuyên vào một xe cát nhỏ, khối lượng $M = 1,5 kg$ đang chuyển động ngược hướng trên mặt ngang với vận tốc $0,5 m/s$ và ngay sau đó đạn nằm yên trong xe. Bỏ qua ma sát giữa xe và mặt đường. Tốc độ của xe sau khi đạn đã nằm yên trong cát là $7,4 m/s$ theo hướng chuyển động ban đầu của viên đạn. Khối lượng của viên đạn là:
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của viên đạn
Gọi \({v_1},{v_2},V\)lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} < = > 7,4 = \dfrac{{{m_1}.600 - 1,5.0,5}}{{{m_1} + 1,5}} < = > {m_1} = 0,02kg = 20g\)
Với $v_2 = -0,5 m/s$ vì xe chuyển động ngược chiều so với viên đạn
Một viên bi thứ nhất có khối lượng $m_1 = 200 g$ chuyển động với vận tốc $v_1 = 4 m/s$ đến va chạm với viên bi thứ hai có khối lượng $m_2$ đang đứng yên. Coi va chạm giữa hai viên bi là hoàn toàn mềm. Cả hai viên bi đều ở trên mặt sàn nằm ngang, không ma sát. Vận tốc của cả hai viên bi sau va chạm bằng $2 m/s$. Khối lượng của viên bi thứ hai là:
Sau va chạm 2 viên bị dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai viên bi
Gọi \({v_1},{v_2},V\) lần lượt là vận tốc của viên bi thứ nhất, viên bi thứ hai và của 2 viên bi sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} < = > 2 = \dfrac{{0,2.4 + {m_2}.0}}{{0,2 + {m_2}}} < = > {m_2} = 0,2\,kg = 200g\)
Một quả cầu khối lượng m1 = 4 kg, chuyển động với vận tốc v1 = 6 m/s, va chạm hoàn toàn mềm với quả cầu thứ 2 có khối lượng m2 = 5 kg đang chuyển động cùng chiều với quả cầu thứ nhất. Cả hai quả cầu đều chuyển động theo phương ngang. Vận tốc của cả hai quả cầu sau va chạm bằng 3,78 m/s. Vận tốc của quả cầu thứ 2 là
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của hai vật
Gọi \({v_1},{v_2},V\)lần lượt là vận tốc của quả cầu 1, quả cầu 2 và hai quả cầu sau va chạm. Ta có:
\({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V = > V = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}} < = > 3,78 = \frac{{4.6 + 5.{v_2}}}{{4 + 5}} < = > {v_2} = 2\,m/s\)
Trên mặt phẳng nằm ngang một hòn bi m1 = 15 g chuyển động sang phải với vận tốc 22,5 cm/s va chạm trực diện đàn hồi với một hòn bi khối lượng m2 = 30 g đang chuyển động sang trái với vận tốc 18 cm/s. Sau va chạm hòn bi m1 đổi chiều chuyển động sang trái với vận tốc 31,5 cm/s. Bỏ qua mọi ma sát, vận tốc của hòn bi m2 sau va chạm là
Hai vật va chạm đàn hồi trực diện. Chọn chiều dương là chiều chuyển động của viên bi 1. Ta có:
\({v_2}' = \frac{{\left( {{m_2} - {m_1}} \right){v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{\left( {0,03 - 0,015} \right).( - 18) + 2.0,015.22,5}}{{0,03 + 0,015}} = 9\,cm/s\)
Với v2 = -18 cm/s vì viên bi 2 chuyển động ngược chiều so với viên bi 1
Hai viên bi có khối lượng m1 = 3kg và m2 = 2kg chuyển động trên mặt phẳng ngang ngược chiều nhau với các vận tốc tương ứng v1 = 1m/s, v2 = 2m/s. Coi va chạm của hai viên bi là hoàn toàn đàn hồi xuyên tâm. Chọn chiều dương là chiều chuyển động ban đầu của viên bi 1. Vận tốc ngay sau va chạm của viên bi 1 và viên bi 2 lần lượt là:
Hai vật va chạm đàn hồi trực diện. Chọn chiều dương là chiều chuyển động của viên bi 1 nên vận tốc của viên bi 2 là: \({v_2} = - 2m/s\) . Ta có:
\({v_1}' = \frac{{\left( {{m_1} - {m_2}} \right){v_1} + 2{m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{\left( {3 - 2} \right).1 - 2.2.2}}{{3 + 2}} = - 1,4m/s\)
\({v_2}' = \frac{{\left( {{m_2} - {m_1}} \right){v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{\left( {2 - 3} \right).( - 2) + 2.3.1}}{{3 + 2}} = 1,6\,m/s\)
Một vật có khối lượng $m$ chuyển động với vận tốc $3 m/s$ đến va chạm với một vật có khối lượng $2m$ đang đứng yên. Coi va chạm giữa hai vật là mềm. Sau va chạm, hai vật dính nhau và chuyển động với cùng vận tốc
Hệ hai vật ngay khi va chạm mềm là một hệ kín nên động lượng của hệ được bảo toàn:
\({m_1}{\overrightarrow v _1} + {m_2}{\overrightarrow v _2} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \)
Do \({v_2} = 0 = > v = \frac{{{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{m.3}}{{m + 2m}} = 1\,m/s\)
Một viên đạn đang bay với vận tốc \(10 m/s\) thì nổ thành hai mảnh. Mảnh thứ nhất, chiếm \(60\%\) khối lượng của quả lựu đạn và tiếp tục bay theo hướng cũ với vận tốc \(25 m/s\). Tốc độ và hướng chuyển động của mảnh thứ hai là:
Ta có:
+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
+ Gọi \(m_1 = 0,6m\) là khối lượng của mảnh thứ nhất
=> Khối lượng của mảnh còn lại là \(m_2=m-m_1=m-0,6m=0,4m\)
+ Áp dụng định luật bảo toàn động lượng ta có:
\(\overrightarrow p=\overrightarrow p_1 + \overrightarrow p_2\)
\(m\overrightarrow v = {m_1}{\overrightarrow v _1} + \left( {m - {m_1}} \right){\overrightarrow v _2}\) (*)
Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ
=> \({\overrightarrow v _1} \uparrow \uparrow \overrightarrow v\)
Từ phương trình (*) ta suy ra:
\({v_2} = \dfrac{{mv - {m_1}{v_1}}}{{m - {m_1}}} = \dfrac{{(10 - 25.0,6)m}}{{(1 - 0,6)m}} = - 12,5\,m/s\)
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Bắn một hòn bi thép với vận tốc v vào một hòn bi thủy tinh đang nằm yên. Sau khi va chạm hai hòn bi cùng chuyển động về phía trước, nhưng bi thủy tinh có vận tốc gấp ba lần vận tốc của bi thép. Tìm vận tốc của mỗi hòn bi sau va chạm. Biết khối lượng bi thép bằng ba lần khối lượng bi thủy tinh.
Khối lượng bi thép bằng ba lần khối lượng bi thuỷ tinh: m1 = 3.m2
Động lượng của hệ trước va chạm: \(\overrightarrow {{p_1}} = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = {m_1}\overrightarrow v + {m_2}\overrightarrow 0 = {m_1}\overrightarrow v \)
Động lượng của hệ sau va chạm: \(\overrightarrow {{p_2}} = {m_1}\overrightarrow {{v_1}'} + {m_2}\overrightarrow {{v_2}'} \)
Áp dụng định luật bảo toàn động lượng cho lúc trước và sau va chạm ta có:
\(\overrightarrow {{p_1}} = \overrightarrow {{p_2}} \Leftrightarrow {m_1}\overrightarrow v = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} \)
Chọn chiều dương là chiều chuyển động của bi thép trước khi va chạm. Ta có:
\({m_1}v = {m_1}{v_1}' + {m_2}{v_2}'\)
Theo bài ra ta có: \(\left\{ \begin{array}{l}{m_1}\; = 3.{m_2}\\{v_2}'\; = {\rm{ }}3.{v_1}'\end{array} \right. \Rightarrow 3{m_2}.v = 3.{m_2}.{v_1}'\; + {\rm{ }}{m_2}.3{v_1}' \Rightarrow \left\{ \begin{array}{l}{v_1}' = \dfrac{v}{2}\\{v_2}' = \dfrac{{3v}}{2}\end{array} \right.\)
Một viên đạn khối lượng 1kg đang bay theo phương thẳng đứng với vận tốc 500m/s thì nổ thành hai mảnh có khối lượng bằng nhau. Mảnh thứ nhất bay theo phương ngang với vận tốc \(500\sqrt 2 m/s\). Hỏi mảnh thứ 2 bay theo phương nào với vận tốc bao nhiêu?
\(\begin{array}{l}m = 1kg;v = 500m/s\\{m_1} = {m_2} = \dfrac{m}{2} = 0,5kg;{v_1} = 500\sqrt 2 m/s\end{array}\)
Xét hệ gồm hai mảnh đạn trong thời gian nổ.
Động lượng của hệ trước khi đạn nổ: \(\overrightarrow p = m.\overrightarrow v \)
Động lượng sau khi đạn nổ: \(\overrightarrow {p'} = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} = {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \)
Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow p = \overrightarrow {p'} \Rightarrow \overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Viên đạn đang bay theo phương thẳng đứng thì nổ thành hai mảnh mảnh thứ nhất bay theo phương ngang. Ta có hình vẽ:
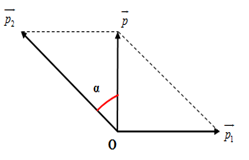
Từ hình vẽ ta có:
\(\begin{array}{l}p_2^2 = {p^2} + p_1^2 \Leftrightarrow {\left( {\dfrac{m}{2}.{v_2}} \right)^2} = {\left( {mv} \right)^2} + {\left( {\dfrac{m}{2}.{v_1}} \right)^2}\\ \Rightarrow v_2^2 = 4{v^2} + v_1^2 = {4.500^2} + {\left( {500\sqrt 2 } \right)^2} \Rightarrow {v_2} = 1225m/s\end{array}\)
Góc hợp bởi giữa \(\overrightarrow {{v_2}} \) và phương thẳng đứng là : \(\sin \alpha = \dfrac{{{p_1}}}{{{p_2}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{500\sqrt 2 }}{{1225}} \Rightarrow \alpha = {35^0}\)

