Một quả cầu bắt đầu lăn từ đỉnh dốc dài 150m, sau 15s nó đến chân dốc. Sau đó tiếp tục đi trên mặt ngang được 75m thì dừng lại. Chọn chiều dương là chiều chuyển động của quả cầu. Thời gian chuyển động của quả cầu từ đỉnh dốc đến khi dừng lại là:

ta có sơ đồ minh họa quá trình chuyển động:

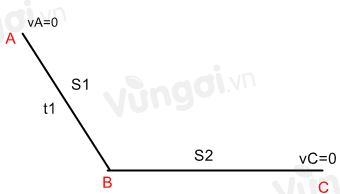
Gia tốc của quả cầu ở chân dốc B là:

\({a_1} = \dfrac{{2\left( {{s_1} - {v_A}{t_1}} \right)}}{{t_1^2}} = \dfrac{{2\left( {150 - 0} \right)}}{{{{15}^2}}} = \dfrac{4}{3}\left( {m/{s^2}} \right)\)

khi đó vận tốc của quả cầu khi ở B là: \({v_B} = {v_A} + {a_1}{t_1} = 0 + \dfrac{4}{3}.15 = 20\left( {m/s} \right)\)

Gia tốc của quả cầu khi chuyển động trên mặt ngang là: \({a^2} = \dfrac{{v_C^2 - v_B^2}}{{2{{\rm{s}}_2}}} = \dfrac{{{0^2} - {{20}^2}}}{{2.75}} = \dfrac{{ - 8}}{3}\left( {m/{s^2}} \right)\)

thời gian quả cầu chuyển động trên mặt ngang là: \({t_2} = \dfrac{{{v_C} - {v_B}}}{{{a_2}}} = \dfrac{{0 - 20}}{{ - \dfrac{8}{3}}} = 7,5{\rm{s}}\)

tổng thời gian chuyển động của quả cầu là: \(t = {t_1} + {t_2} = 15 + 7,5 = 22,5{\rm{s}}\)