Câu hỏi:
1 năm trước
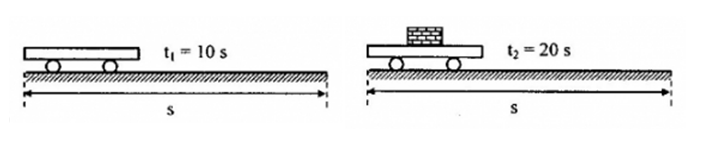
Một xe lăn khối lượng 50kg, dưới tác dụng của một lực kéo theo phương ngang chuyển động không vận tốc đầu từ đầu phòng đến cuối phòng mất 10s. Khi chất lên xe một kiện hàng, xe phải chuyển động mất 20s. Bỏ qua ma sát. Khối lượng của kiện hàng là:
Trả lời bởi giáo viên
Đáp án đúng: b
Gọi m và m’ lần lượt là khối lượng của xe và của kiện hàng.
Chọn chiều dương là chiều chuyển động của xe
+ Áp dụng định luật II Niutơn:
- cho xe: \({a_1} = \frac{F}{m}\) (1)
- cho xe và kiện hàng: \({a_2} = \frac{F}{{m + m'}}\) (2)
+ Quãng đường đi của xe trong hai trường hợp là: \(s = \frac{1}{2}{a_1}t_1^2 = \frac{1}{2}{a_2}t_2^2\) (3)
Từ (3), ta suy ra: \(\frac{{{a_1}}}{{{a_2}}} = \frac{{t_2^2}}{{t_1^2}} = \frac{{{{20}^2}}}{{{{10}^2}}} = 4\)
Từ (1) và (2), ta suy ra: \(\frac{{{a_1}}}{{{a_2}}} = \frac{{m + m'}}{m} \to m' = 3m = 3.50 = 150kg\)
Hướng dẫn giải:
+ Vận dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)
+ Vận dụng biểu thức quãng đường: \(s = {s_0} + {v_0}t + \frac{1}{2}a{t^2}\)
Câu hỏi khác
- Bài tập trắc nghiệm Định luật 3 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Trọng lực và lực căng môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Định luật 2 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Tổng hợp và phân tích lực. Cân bằng lực môn Vật lí lớp 10 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Định luật 1 Newton môn Vật lí lớp 10 sách KNTTVCS có lời giải
