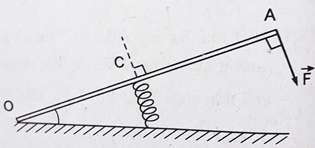
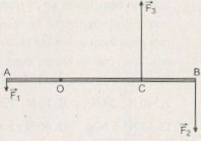
Một thanh cứng AB dài \(7m\), có khối lượng không đáng kể, có trục quay O, hai đầu chịu 2 lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) như hình. Cho \({F_1} = 50N\); \({F_2} = 200N\) và \(OA = 2m\) . Đặt vào thanh một lực \({F_3}\) hướng lên và có độ lớn \(300N\) để cho thanh nằm ngang. Khoảng cách OC là

Dưới tác dụng của lực \(\overrightarrow F \) như hình. Thanh AB có thể quay quanh điểm A. Cánh tay đòn của lực \(\overrightarrow F \) trong trường hợp này bằng bao nhiêu? Biết \(AB = 5cm\).

Tính momen của lực \(\overrightarrow F \) đối với trục quay O, cho biết \(F = 100N\), \(OA = 100cm\). Bỏ qua trọng lượng của thanh.

Một thanh đồng chất có trọng lượng \(P\) được gắn vào tường nhờ một bản lề và được giữ nằm ngang bằng một dây treo thẳng đứng như hình. Xét momen lực đối với bản lề. Hãy chọn câu đúng.

Một thanh dài \(L\), trọng lượng \(P\), được treo nằm ngang vào tường như hình.

Một vật có trọng lượng \({P_1}\) được treo ở đầu thanh. Dây treo làm với thanh một góc \(\alpha \). Lực căng của dây bằng

Một bàn đạp có trọng lượng không đáng kể, có chiều dài \(OA = 20cm\), quay dễ dàng quanh trục O nằm ngang như hình. Một lò xo gắn vào điểm giữa C. Người ta tác dụng lên bàn đạp tại điểm A một lực \(\overrightarrow F \) vuông góc với bàn đạp và có độ lớn \(20N\). Bàn đạp ở trạng thái cân bằng khi lò xo có phương vuông góc với OA và bị ngắn đi một đoạn \(8cm\) so với khi không bị nén. Lực của lò xo tác dụng lên bàn đạp và độ cứng của lò xo là:

Một người nâng một tấm gỗ nặng \(30kg\) dài \(1,5m\), lực nâng vuông góc với tấm gỗ và giữ cho nó hợp với mặt đất nằm ngang một góc \(\alpha  = {30^0}\). Biết trọng tâm của tấm gỗ cách đầu mà người đó nâng \(120cm\). Tính lực nâng của người đó.