Thanh AB dài 10m có khối lượng 7kg và có trọng tâm cách đầu A một đoạn 2m như hình vẽ. Thanh có thể quay quanh một trục O cách đầu A một đoạn 3m, lấy g = 10m/s2. Phải tác dụng vào đầu B một lực \(\overrightarrow {\rm{F}} \) bằng bao nhiêu để thanh AB nằm cân bằng theo phương ngang
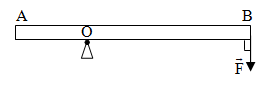
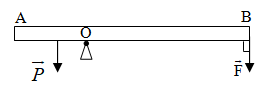
Trọng tâm là điểm đặt của trọng lực, để thanh cân bằng thì \(P.{d_1} = F.{d_2} < = > mg{d_1} = F{d_2} < = > 7.10.(3 - 2) = F.(10 - 3) < = > F = 10N\)
Thanh AB đồng chất, tiết diện đều có khối lượng $1kg$ được treo bằng $1$ sợi dây nhẹ BC như hình vẽ. Một đầu thanh được tì vuông góc vào bức tường tại điểm A, lấy $g = 10m/s^2$, \({\rm{\alpha = 3}}{{\rm{0}}^{\rm{0}}}\). Lực căng của dây BC là
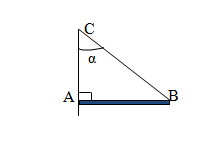
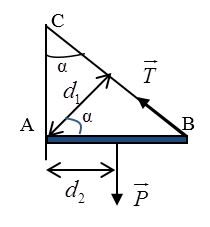
Quy tắc mômen lực:
\(T{d_1} = P{d_2}\) (1)
Từ hình ta có: \(\left\{ \begin{array}{l}{d_1} = ABcos\alpha \\{d_2} = \dfrac{{AB}}{2}\end{array} \right.\)
Thay vào (1) ta được:
\(\begin{array}{l} \leftrightarrow T.AB.\cos \alpha = m.g.\dfrac{{AB}}{2}\\ \leftrightarrow T = \dfrac{{\dfrac{{mg}}{2}}}{{\cos \alpha }} = \dfrac{{\dfrac{{1.10}}{2}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{10}}{{\sqrt 3 }}\,N\end{array}\)
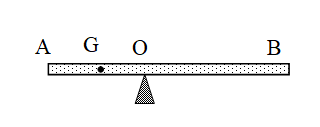
Một thanh AB tiết diện đều, đồng chất dài 90cm, nặng 2kg, móc vào đầu A của thanh 1 vật có khối lượng 4kg, đầu B một vật có khối lượng 6kg. Thanh AB được đặt nằm ngang lên một giá đỡ O như vẽ. Xác định vị trí của giá đỡ O để thanh AB nằm cân bằng theo phương ngang
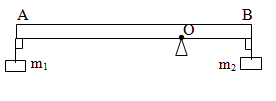
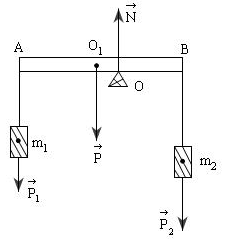
Gọi \({O_1}\) là trọng tâm của thanh \(AB\) ,\({O_1}\) là trung điểm của \(AB\)
Giả sử đặt giá đỡ tại điểm \(O\) trong khoảng \({O_1}B\) ( vì \({P_2} > {P_1}\) nên giả thiết này là hợp lí). Các lực tác dụng lên thanh \(AB\) là: các trọng lực \(\overrightarrow P ,\overrightarrow {{P_1}} ,\overrightarrow {{P_2}} \), đặt tại \({O_1},A,B\) và phản lực \(\overrightarrow N \) của giá đỡ \(O\)
Vì thanh \(AB\) có thể quay xung quanh trục đi qua \(O\) nên muốn cho thanh \(AB\) nằm cân bằng ta áp dụng quy tắc mômen đối với trục quay \(O\) ( và lưu ý rằng momen của \(\overrightarrow N \) đối với \(O\) bằng không):
\(\begin{array}{l}M\left( P \right) + M\left( {{P_1}} \right) = M\left( {{P_2}} \right)\\P.O{O_1} + {P_1}.OA = {P_2}.OB\\P\left( {OA - A{O_1}} \right) + {P_1}.OA = {P_2}\left( {AB.OA} \right)\end{array}\)
Suy ra \(OA = \frac{{P.A{O_1} + {P_2}.AB}}{{P + {P_1} + {P_2}}} = \frac{{m.A{O_1} + {m_2}.AB}}{{m + {m_1} + {m_2}}}\)
Thay số ( \(AB = 90cm,A{O_1} = 45cm\) ) ta được \(OA = 52,5{\rm{ }}cm\)
Muốn cho thanh nằm cân bằng phải đặt thanh lên giá đỡ tại điểm O cách đầu A là 52,5cm
Một thanh $AB$ có trọng lượng \(150\left( N \right)\) có trọng tâm $G$ chia đoạn $AB$ theo tỉ lệ \(BG = 2AG\). Đầu $B$ của thanh được treo lên trần bằng dây nhẹ, không giãn. Đầu $A$ có thể quay quanh trục nằm ngang. Thanh $AB$ hợp với phương ngang góc $α$ (hình vẽ). Tính lực căng dây T?
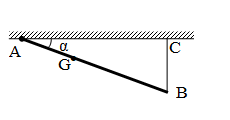
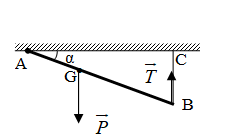
Vật cân bằng, ta suy ra tổng quy tắc mônmen lực của vật bằng 0.
\(P.AG\cos \alpha = T.AB\cos \alpha \\< = > P.AG\cos \alpha = T.3AG\cos \alpha \\< = > P = 3T < = > T = 50N\)
Thanh OA có khối lượng không đáng kể, chiều dài \(20\left( {cm} \right)\), quay dễ dàng quanh trục nằm ngang O. Một lò xo gắn vào trung điểm C của thanh. Người ta tác dụng vào đầu A của thanh một lực \(F = 20\left( N \right)\), vuông góc với thanh và hướng xuống. Khi thanh ở trạng thái cân bằng, trục lò xo vuông góc với OA. Biết lò xo ngắn đi \(8\left( {cm} \right)\) so với lúc không bị nén (hình vẽ). Tính độ cứng của lò xo?
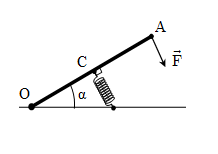
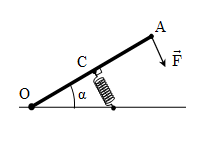
Khi lò xo bị biến dạng sẽ xuất hiện lực đàn hồi. Áp dụng quy tắc mômen lực:
\({F_{dh}}{d_1} = F{d_2} < = > {F_{dh}} = 2F < = > {F_{dh}} = 40N\)
Mặt khác: \({F_{dh}} = k.\Delta l < = > 40 = k.0,08 < = > k = 500\,N/m\)
Có đòn bẩy như hình 10. Đầu A của đòn bẩy treo một vật có trọng lượng \(30\left( N \right)\). Chiều dài đòn bẩy dài \(50\left( {cm} \right)\). Khoảng cách từ đầu A đến trục quay O là \(20\left( {cm} \right)\). Vậy đầu B của đòn bẩy phải treo một vật khác có trọng lượng là bao nhiêu để đòn bẩy cân bằng theo phương ngang? (Bỏ qua khối lượng đòn bẩy)
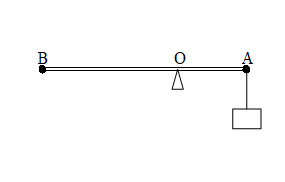
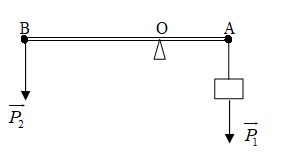
Quy tắc mômen lực: \({P_2}.OB = {P_1}.OA < = > {P_2}(50 - 20) = 30.20 < = > {P_2} = 20\,N\)
Một người nâng một đầu của một thanh gỗ thẳng, đồng chất, tiết diện đều có khối lượng \(m = 20\left( {kg} \right)\) lên cao hợp với phương nằm ngang một góc α. Lấy \(g = 10\left( {m/{s^2}} \right)\) (hình vẽ). Tính độ lớn của lực nâng \(\vec F\) của người đó?
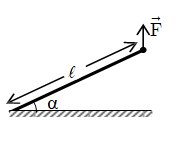
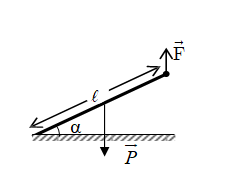
Vì thanh có khối lượng nên sẽ bị tác dụng bởi trọng lực đặt tại trung điểm của thanh
Quy tắc mômen lực: \(P.\frac{l}{2} = F.l < = > P/2 = F < = > mg/2 = F < = > 20.10/2 = F < = > F = 100\,N\)
Một thanh sắt dài đồng chất, tiết diện đều được đặt trên mặt bàn sao cho 1/4 chiều dài của nó nhô ra khỏi mặt bàn (hình vẽ). Tác dụng vào đầu nhô ra một lực F hướng thẳng đứng xuống dưới. Khi lực tác dụng đạt tới giá trị 120 N thì đầu kia của thanh sắt bắt đầu bênh lên. Hỏi trọng lượng của thanh sắt là
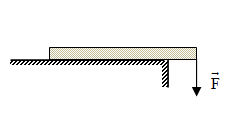
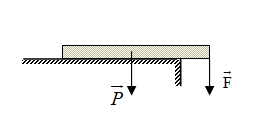
Vì thanh có khối lượng nên sẽ bị tác dụng của trọng lực và có điểm đặt tại trung điểm của thanh
Quy tắc mômen lực:\(P{d_1} = F{d_2} < = > Pl/4 = Fl/4 < = > P = F = 120N\)
Vậy trọng lượng của thanh là 120N
Một chiếc xà ngang AB có tiết diện đều, đồng chất dài $1m$ có khối lượng $20kg$. Một đầu xà gắn vuông góc vào tường, đầu kia được treo bằng một sợi dây như hình vẽ. Biết góc hợp bởi dây và phương ngang là \({\rm{\alpha = 6}}{{\rm{0}}^{\rm{0}}}\). Lấy $g = 10m/s^2$. Lực căng của sợi dây BC là:
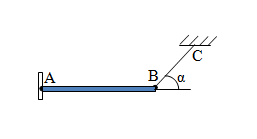
Vì thanh có khối lượng nên sẽ bị tác dụng của trọng lực và có điểm đặt tại trung điểm của thanh
Vẽ hình ta được:
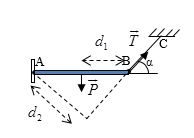
Quy tắc mômen lực:
\(P.{d_1} = T.{d_2} < = > mg{d_1} = T{d_2} < = > mg\frac{{AB}}{2} = T.AB\sin \alpha < = > 20.10.0,5 = T\sin 60 < = > T = \frac{{200}}{{\sqrt 3 }}\,N\)
Một thanh chắn đường dài AB có chiều dài 7,8 m; trọng lượng 420 N và có trọng tâm cách đầu A của thanh 1,2 m. Thanh có thể quay quanh một trục O nằm ngang ở cách đầu A một khoảng 1,5 m như hình vẽ. Để giữ thanh nằm ngang ta phải tác dụng lên đầu B của thanh một lực có độ lớn bao nhiêu
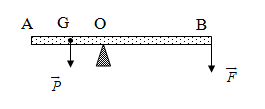
Quy tắc mômen lực:
\(P{{\rm{d}}_1} = F{d_2} < = > P.OG = F.OB < = > 420.(1,5 - 1,2) = F.(7,8 - 1,5) < = > F = 20N\)

