Công của lực ma sát khi vật chuyển động được \(5s\) là:
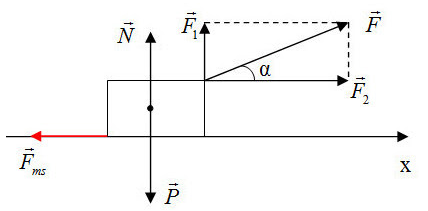
+ Chọn chiều dương là chiều chuyển động của vật
Theo định luật II – Newton ta có: \(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) (1)
+ Chiếu (1) theo các phương, ta được:
- Theo phương Oy: \(N + {F_1} = P \Rightarrow N = P - {F_1}\)
Có \({F_1} = F\sin \alpha \) ta suy ra \(N = P - F\sin \alpha \)
- Theo phương Ox: \({F_2} - {F_{ms}} = ma\)
Có \({F_2} = F\cos \alpha \), ta suy ra \(Fcos\alpha - {F_{ms}} = ma\)
Lại có, lực ma sát
\(\begin{array}{l}{F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\\ = \mu \left( {mg - F\sin \alpha } \right)\\ = 0,2\left( {2.10 - 10.\sin {{30}^0}} \right)\\ = 3N\end{array}\)
Ta suy ra:
\(\begin{array}{l}Fcos\alpha - {F_{ms}} = ma\\ \Leftrightarrow Fcos\alpha - \mu \left( {mg - F\sin \alpha } \right) = ma\\ \Leftrightarrow 10.cos{30^0} - 0,2.\left( {2.10 - 10.\sin {{30}^0}} \right) = 2.a\\ \Rightarrow a = 2,83m/{s^2}\end{array}\)
+ Quãng đường vật di chuyển được từ lúc ban đầu cho đến \(5s\) là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.2,{83.5^2} = 35,375m\)
+ Ta có, góc hợp bởi hướng của lực ma sát và phương chuyển dời của vật là: \({180^0}\)
=> Công của lực ma sát khi vật chuyển động được \(5s\) là: \({A_{{F_{ms}}}} = {F_{ms}}.s.cos{180^0} = 3.35,375.c{\rm{os18}}{{\rm{0}}^0} = - 106,125N\)
Công của lực F khi vật chuyển động được \(5s\) là:
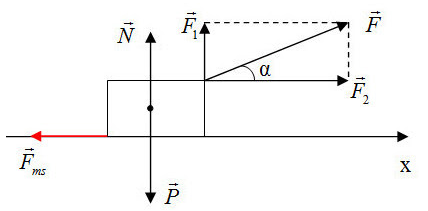
+ Chọn chiều dương là chiều chuyển động của vật
Theo định luật II – Newton ta có: \(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) (1)
+ Chiếu (1) theo các phương, ta được:
- Theo phương Oy: \(N + {F_1} = P \Rightarrow N = P - {F_1}\)
Có \({F_1} = F\sin \alpha \) ta suy ra \(N = P - F\sin \alpha \)
- Theo phương Ox: \({F_2} - {F_{ms}} = ma\)
Có \({F_2} = F\cos \alpha \), ta suy ra \(Fcos\alpha - {F_{ms}} = ma\)
Lại có, lực ma sát \({F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\)
Ta suy ra:
\(\begin{array}{l}Fcos\alpha - {F_{ms}} = ma\\ \Leftrightarrow Fcos\alpha - \mu \left( {mg - F\sin \alpha } \right) = ma\\ \Leftrightarrow 10.cos{30^0} - 0,2.\left( {2.10 - 10.\sin {{30}^0}} \right) = 2.a\\ \Rightarrow a = 2,83m/{s^2}\end{array}\)
+ Quãng đường vật di chuyển được từ lúc ban đầu cho đến \(5s\) là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.2,{83.5^2} = 35,375m\)
+ Công của lực F khi vật chuyển động được 5s là: \({A_F} = Fs.c{\rm{os}}\alpha = 10.35,375.cos{30^0} \approx 306,4J\)
Công của lực F khi vật chuyển động được \(5s\) là:

+ Chọn chiều dương là chiều chuyển động của vật
Theo định luật II – Newton ta có: \(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) (1)
+ Chiếu (1) theo các phương, ta được:
- Theo phương Oy: \(N + {F_1} = P \Rightarrow N = P - {F_1}\)
Có \({F_1} = F\sin \alpha \) ta suy ra \(N = P - F\sin \alpha \)
- Theo phương Ox: \({F_2} - {F_{ms}} = ma\)
Có \({F_2} = F\cos \alpha \), ta suy ra \(Fcos\alpha - {F_{ms}} = ma\)
Lại có, lực ma sát \({F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\)
Ta suy ra:
\(\begin{array}{l}Fcos\alpha - {F_{ms}} = ma\\ \Leftrightarrow Fcos\alpha - \mu \left( {mg - F\sin \alpha } \right) = ma\\ \Leftrightarrow 10.cos{30^0} - 0,2.\left( {2.10 - 10.\sin {{30}^0}} \right) = 2.a\\ \Rightarrow a = 2,83m/{s^2}\end{array}\)
+ Quãng đường vật di chuyển được từ lúc ban đầu cho đến \(5s\) là: \(s = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.2,{83.5^2} = 35,375m\)
+ Công của lực F khi vật chuyển động được 5s là: \({A_F} = Fs.c{\rm{os}}\alpha = 10.35,375.cos{30^0} \approx 306,4J\)
Kéo một xe goòng bằng một sợi dây cáp với một lực bằng \(150N\). Góc giữa dây cáp và mặt phẳng ngang bằng \({30^0}\). Công của lực tác dụng lên xe để xe chạy được \(200m\) có giá trị
Công của lực tác dụng lên xe có giá trị:
\(A = F.s.cos\alpha = 150.200.cos{30^0} = 25980J\)
Vật nào sau đây có khả năng sinh công?
Ta có: Khi lực \(\overrightarrow F \) không đổi tác dụng lên một vật và điểm đặt của lực đó chuyển dời một đoạn s theo hướng hợp với hướng của lực góc \(\alpha \) thì công thực hiện bởi lực đó được tính theo công thức:
\(A = F{\rm{scos}}\alpha \)
=>Phương án B: Chiếc bút đang rơi là vật có khả năng sinh công
(Chiếc bút đang rơi chịu tác dụng của trọng lực của chiếc bút và nó dịch chuyển (chuyển dời) xuống dưới theo hướng của trọng lực tác dụng lên nó)
Chọn câu sai?
Công suất là:
Phát biểu sai về công suất là: Công suất là đại lượng cho biết công thực hiện được nhiều hay ít của người, máy, công cụ…
Lực tác dụng lên một vật đang chuyển động thẳng biến đổi đều thực hiện công khi:
Từ biểu thức tính công: \(A = F{\rm{scos}}\alpha \)
Ta suy ra: Lực tác dụng lên một vật đang chuyển động thẳng biến đổi đều không thực hiện công khi lực có phương vuông góc với gia tốc hoặc vận tốc của vật.
=> Các phương án A, B, C – vật không thực hiện công
Phương án D – vật thực hiện công \(A = Fs\) (do \(\alpha = {0^0}\))
Đơn vị nào dưới đây là đơn vị của công suất?
B – đúng
A, C, D – sai vì: Đơn vị của công suất là J/s hoặc W hoặc HP, CV (mã lực)
Phát biểu nào sau đây là không đúng?
Ta có:
+ Công suất: \(P = \dfrac{A}{t}\)
+ Hiệu suất: \(H = \dfrac{{A'}}{A}\)
Mặt khác, hiệu suất \(H \le 1\)
Từ đó, ta suy ra các phương án
A, C, D
B – sai vì: Hiệu suất của máy luôn nhỏ hơn hoặc bằng 1
Tác dụng lực không đổi \(150N\) theo phương hợp với phương ngang góc \({30^0}\) vào vật khối lượng m làm vật chuyển động được quãng đường \(20m\). Công của lực tác dụng có giá trị
Ta có góc tạo bởi hướng của lực và phương chuyển động s là \(\alpha = \left( {\widehat {\overrightarrow F ,\overrightarrow s }} \right) = {30^0}\)
=> Công của lực tác dụng: \(A = Fs\cos \alpha = 150.20.cos{30^0} \approx 2598J\)
Thả rơi một hòn sỏi khối lượng 50 g từ độ cao 1,2 m phía trên miệng giếng xuống một giếng sâu 3 m. Công của trọng lực khi vật rơi chạm đáy giếng là (Lấy g = 10 m/s2)
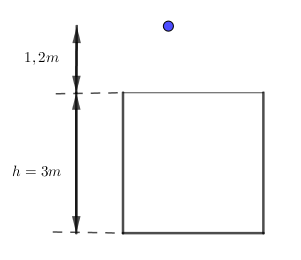
Ta có,
+ Góc hợp bởi véctơ lực và véctơ chuyển dời: \(\alpha = {0^0}\)
+ Quãng đường vật rơi là: \(s = h + 1,2 = 3 + 1,2 = 4,2m\)
+ Công của trọng lực khi vật rơi chạm đáy giếng là:
\(A = P{\rm{s}}.c{\rm{os}}\alpha = P{\rm{s}} = mg{\rm{s}} = 0,05.10.4,2 = 2,1J\)
Một động cơ điện cung cấp công suất 30kW cho một cần cẩu nâng một toa hàng có khối lượng 1000 kg lên cao 15m. Lấy \(g = 10{\rm{ }}m/{s^2}\). Thời gian tối thiểu để thực hiện công việc đó là
Ta có:
+ Công nâng vật lên độ cao \(s = 15m\) là: \(A = F{\rm{scos}}\alpha \)
Với lực nâng vật \(F \ge P = mg = 1000.10 = 10000N\)
\(\alpha = {0^0}\)
Ta suy ra công nâng vật: \(A \ge P.s = 10000.15 = 150000J\)
+ Công suất: \(P = \dfrac{A}{t}\)
Ta suy ra thời gian \(t = \dfrac{A}{P}\)
Có \(A \ge 150000J\)
Suy ra \(t \ge \dfrac{A}{P} = \dfrac{{150000}}{{{{30.10}^3}}} = 5s\)
Vậy thời gian tối thiểu để thực hiện công việc đó là 5s
Một ôtô có khối lượng \(1,5\) tấn tắt máy chuyển động chậm dần đều từ vận tốc ban đầu \(10m/s\) dưới tác dụng của lực ma sát. Công suất của lực ma sát từ lúc ô tô tắt máy cho đến lúc dừng lại là bao nhiêu? Biết hệ số ma sát \(0,2\), cho \(g = 10m/{s^2}\)
+ Chọn chiều dương là chiều chuyển động của xe sau khi tắt máy
Áp dụng biểu thức định luật II – Newton, ta có: \(\overrightarrow {{F_{ms}}} = m\overrightarrow a \)
Chiếu theo chiều dương đã chọn, ta được
\(\begin{array}{l} - {F_{ms}} = ma \Leftrightarrow - \mu mg = ma\\ \Rightarrow a = - \mu g = - 0,2.10 = - 2m/{s^2}\end{array}\)
+ Ta có vận tốc ban đầu của xe \({v_0} = 10m/s\) khi xe dừng lại vận tốc của xe \(v = 0m/s\)
Áp dụng hệ thức liên hệ, ta có: \({v^2} - v_0^2 = 2as\)
=> Quãng đường xe chuyển động từ khi tắt máy đến khi dừng lại là: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {{10}^2}}}{{2.\left( { - 2} \right)}} = 25m\)
+ Ta có phương trình vận tốc từ khi xe tắt máy: \(v = {v_0} + at = 10 - 2t\)
=> Thời gian từ lúc ô tô tắt máy đến khi dừng lại: \(t = \dfrac{{v - {v_0}}}{a} = \dfrac{{0 - 10}}{{ - 2}} = 5s\)
+ Công của lực ma sát:
\(\begin{array}{l}A = {F_{ms}}.s.c{\rm{os18}}{{\rm{0}}^0} = \mu mg.s\cos {180^0}\\ = 2.\left( {1,5.100} \right).10.25.cos{180^0} = - 75000J\end{array}\)
+ Công suất của lực ma sát từ lúc ô tô tắt máy đến khi dừng lại: \(P = \dfrac{{\left| A \right|}}{t} = \dfrac{{75000}}{5} = 15000J/s\)
Xe chạy trên đường nằm ngang với tốc độ \(60km/h\). Đến quãng đường dốc lực cản tăng gấp 2 lần nên người đó tăng ga tối đa thì công suất tăng lên \(1,5\) lần. Tốc độ tối đa khi xe lên dốc
+ Gọi \({F_1}\) - lực kéo của ô tô trên đoạn đường nằm ngang
\({F_C}\) - lực cản trên đoạn đường nằm ngang
\({P_1}\) - công suất động cơ ô tô trên đoạn đường nằm ngang
\({F_2}\) - lực kéo khi lên dốc
\({F_C}' = 2{F_C}\)
\({v_2}\) - vận tốc khi ô tô lên dốc
\({P_2}\) - công suất tối đa khi lên dốc
+ Ta có, trên đoạn nằm ngang ô tô chạy đều:
Ta suy ra \({F_1} = {F_C}\)
Công suất khi này: \({P_1} = {F_1}{v_1}\)
+ Khi lên dốc ô tô vẫn chuyển động đều, ta suy ra: \({F_2} = {F_C}' = 2{F_C}\)
Mặt khác, có \({P_2} = {F_C}'{v_2} = 2{F_C}{v_2}\)
Lại có: \({F_C} = {F_1}\)
Suy ra: \({P_2} = 2{F_1}{v_2}\)
Theo đề bài, ta có:
\(\begin{array}{l}{P_2} = 1,5{P_1} \Leftrightarrow 2{F_1}{v_2} = 1,5{F_1}{v_1}\\ \Rightarrow {v_2} = \dfrac{{1,5{v_1}}}{2} = \dfrac{{1,5.60}}{2} = 45km/h\end{array}\)
Một thang máy có khối lượng \(m = 3\) tấn đi lên với gia tốc \(a = 1m/{s^2}\). Trong thời gian 4 giây đầu tiên công suất của thang máy là: (cho \(g = 10m/{s^2}\)).
Ta có: \(\left\{ \begin{array}{l}m = 3T = 3000kg\\a = 1m/{s^2}\\g = 10m/{s^2}\\t = 4s\end{array} \right.\)
Biểu diễn các lực tác dụng lên thang máy:
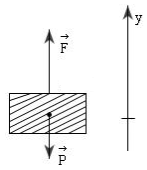
Áp dụng định luật II Niuton ta có: \(\overrightarrow F + \overrightarrow P = m.\overrightarrow a \,\,\left( * \right)\)
Chiếu (*) lên Oy ta có:
\(\begin{array}{l}F - P = ma \Rightarrow F = P + ma = m\left( {g + a} \right)\\ \Rightarrow F = 3000.\left( {10 + 1} \right) = 33000N\end{array}\)
Quãng đường vật đi được trong 4s đầu tiên là:
\(s = {v_0}t + \dfrac{1}{2}a{t^2} = 0 + \dfrac{1}{2}{.1.4^2} = 8m\)
Công của lực kéo thang trong 4s đầu:
\(A = F.s.\cos \left( {\overrightarrow F ;\overrightarrow s } \right) = 33000.8.\cos 0 = 264\,000J\)
Công suất trung bình của lực kéo thang:
\(P = \dfrac{A}{t} = \dfrac{{264000}}{4} = 66000W = 66kW\)
Thác nước cao \(30m\), mỗi giây đổ xuống \(300{m^3}\) nước. Lợi dụng thác nước có thể xây dựng trạm thủy điện công suất bao nhiêu? Biết hiệu suất của trạm thủy điện là \(75\% \), khối lượng riêng của nước \(D = 1000kg/{m^3}\)
Gọi \({V_0}\left( {{m^3}} \right)\) và \({m_0}\left( {kg} \right)\) lần lượt là thể tích và khối lượng nước đổ xuống trong mỗi giây
\(H\) - hiệu suất của động cơ
Ta có:
+ Công suất toàn phần: \({P_{tp}} = \dfrac{{{A_P}}}{t} = \dfrac{{mgh}}{t}\)
Có khối lượng \(m = {m_0}t\)
Suy ra: \({P_{tp}} = \dfrac{{\left( {{m_0}t} \right).gh}}{t} = {m_0}gh = D{V_0}.gh\)
+ Công suất của trạm thủy điện (bằng công suất có ích): \({P_i} = H.{P_{tp}} = H.D{V_0}gh\)
Thay số vào ta được: \({P_i} = 0,75.1000.300.10.30 = 67500000W = 67,5MW\)
Công của lực ma sát tác dụng lên vật đến khi dừng lại là
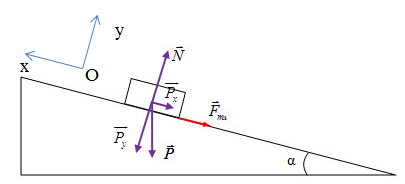
+ Theo định luật II – Newton, ta có: \(\overrightarrow {{F_{ms}}} + \overrightarrow N + \overrightarrow P = m\overrightarrow a \) (1)
Chọn chiều dương là chiều chuyển động của vật (vật đang chuyển động lên trên mặt phẳng nghiêng)
Gắn hệ trục tọa độ như hình
+ Chiếu (1) theo các phương ta được:
- Theo phương Oy: \(N - {P_y} = 0 \Rightarrow N = {P_y} = Pcos\alpha \)
- Theo phương Ox: \( - {F_{ms}} - {P_x} = ma\) (2)
Ta có: \(\left\{ \begin{array}{l}{F_{ms}} = \mu N = \mu P\cos \alpha = 0,2.2.10.c{\rm{os3}}{{\rm{0}}^0} = 2\sqrt 3 N\\{P_x} = P\sin \alpha = mg\sin \alpha = 2.10.\sin {30^0} = 10N\end{array} \right.\)
Thay vào (2) ta được:
\(\begin{array}{l} - 2\sqrt 3 - 10 = ma\\ \Rightarrow a = \dfrac{{ - 2\sqrt 3 - 10}}{2} = - 6,73m/{s^2}\end{array}\)
+ Ta có vận tốc ban đầu của vật \({v_0} = 4m/s\), khi vật dừng lại \(v = 0\)
Áp dụng hệ thức liên hệ ta có: \({v^2} - v_0^2 = 2as\)
=> Quãng đường mà vật đi được đến khi dừng lại là: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {4^2}}}{{2.\left( { - 6,73} \right)}} \approx 1,19m\)
+ Góc hợp bởi lực ma sát và phương dịch chuyển của vật là \({180^0}\)
=> Công của lực ma sát tác dụng lên vật: \({A_{{F_{ms}}}} = {F_{ms}}.s.cos{180^0} = 2\sqrt 3 .1,19.cos{180^0} = - 4,12J\)
Công của trọng lực tác dụng lên vật đến khi dừng lại là
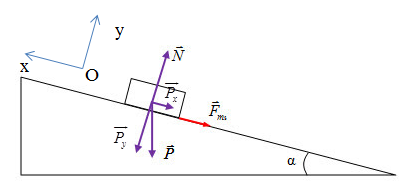
+ Theo định luật II – Newton, ta có: \(\overrightarrow {{F_{ms}}} + \overrightarrow N + \overrightarrow P = m\overrightarrow a \) (1)
Chọn chiều dương là chiều chuyển động của vật (vật đang chuyển động lên trên mặt phẳng nghiêng)
+ Chiếu (1) theo các phương ta được:
- Theo phương Oy: \(N - {P_y} = 0 \Rightarrow N = {P_y} = Pcos\alpha \)
- Theo phương Ox: \( - {F_{ms}} - {P_x} = ma\) (2)
Ta có: \(\left\{ \begin{array}{l}{F_{ms}} = \mu N = \mu P\cos \alpha = 0,2.2.10.c{\rm{os3}}{{\rm{0}}^0} = 2\sqrt 3 N\\{P_x} = P\sin \alpha = mg\sin \alpha = 2.10.\sin {30^0} = 10N\end{array} \right.\)
Thay vào (2) ta được:
\(\begin{array}{l} - 2\sqrt 3 - 10 = ma\\ \Rightarrow a = \dfrac{{ - 2\sqrt 3 - 10}}{2} = - 6,73m/{s^2}\end{array}\)
+ Ta có vận tốc ban đầu của vật \({v_0} = 4m/s\), khi vật dừng lại \(v = 0\)
Áp dụng hệ thức liên hệ ta có: \({v^2} - v_0^2 = 2as\)
=> Quãng đường mà vật đi được đến khi dừng lại là: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {4^2}}}{{2.\left( { - 6,73} \right)}} \approx 1,19m\)
+ Góc hợp bởi phương dịch chuyển và hướng của \(\overrightarrow P \) là \({90^0} + {30^0} = {120^0}\)
=> Công của trọng lực tác dụng lên vật:
\(\begin{array}{l}{A_P} = P.s.c{\rm{os12}}{{\rm{0}}^0} = mg.s.cos{120^0}\\ = 2.10.1,19.c{\rm{os12}}{{\rm{0}}^0} = - 11,9J\end{array}\)
Công của trọng lực tác dụng lên vật đến khi dừng lại là

+ Theo định luật II – Newton, ta có: \(\overrightarrow {{F_{ms}}} + \overrightarrow N + \overrightarrow P = m\overrightarrow a \) (1)
Chọn chiều dương là chiều chuyển động của vật (vật đang chuyển động lên trên mặt phẳng nghiêng)
+ Chiếu (1) theo các phương ta được:
- Theo phương Oy: \(N - {P_y} = 0 \Rightarrow N = {P_y} = Pcos\alpha \)
- Theo phương Ox: \( - {F_{ms}} - {P_x} = ma\) (2)
Ta có: \(\left\{ \begin{array}{l}{F_{ms}} = \mu N = \mu P\cos \alpha = 0,2.2.10.c{\rm{os3}}{{\rm{0}}^0} = 2\sqrt 3 N\\{P_x} = P\sin \alpha = mg\sin \alpha = 2.10.\sin {30^0} = 10N\end{array} \right.\)
Thay vào (2) ta được:
\(\begin{array}{l} - 2\sqrt 3 - 10 = ma\\ \Rightarrow a = \dfrac{{ - 2\sqrt 3 - 10}}{2} = - 6,73m/{s^2}\end{array}\)
+ Ta có vận tốc ban đầu của vật \({v_0} = 4m/s\), khi vật dừng lại \(v = 0\)
Áp dụng hệ thức liên hệ ta có: \({v^2} - v_0^2 = 2as\)
=> Quãng đường mà vật đi được đến khi dừng lại là: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {4^2}}}{{2.\left( { - 6,73} \right)}} \approx 1,19m\)
+ Góc hợp bởi phương dịch chuyển và hướng của \(\overrightarrow P \) là \({90^0} + {30^0} = {120^0}\)
=> Công của trọng lực tác dụng lên vật:
\(\begin{array}{l}{A_P} = P.s.c{\rm{os12}}{{\rm{0}}^0} = mg.s.cos{120^0}\\ = 2.10.1,19.c{\rm{os12}}{{\rm{0}}^0} = - 11,9J\end{array}\)
Một ô tô chạy trên đường nằm ngang với vận tốc \(v = 72km/h\). Công suất của động cơ là \(P = 60kW\). Lực phát động của động cơ là:
Ta có: \(\left\{ \begin{array}{l}v = 72km/h = 20m/s\\P = 60kW = 60000W\end{array} \right.\)
Công suất được xác định bởi công thức:
\(P = F.v \Rightarrow F = \dfrac{P}{v} = \dfrac{{60000}}{{20}} = 3000N\)

