Ở nơi có gia tốc rơi tự gio là $g$, từ độ cao $h$ so với mặt đất, một vật được ném ngang với tốc độ ban đầu $v$. Tầm bay của vật là:
Tầm xa: \(L = v\sqrt {\dfrac{{2h}}{g}} \)
Quỹ đạo của chuyển động ném ngang là:
Phương trình quỹ đạo của vật ném ngang: \(y = \dfrac{g}{{2v_0^2}}{x^2}\)
=> quỹ đạo của chuyển động ném ngang là một đường parabol
Một vật được ném ngang ở độ cao h so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Sau \(5s\) vật chạm đất. Độ cao h bằng:
Ta có, thời gian chạm đất của vật ném ngang: \(t = \sqrt {\frac{{2h}}{g}} \)
Ta suy ra: \(h = \frac{1}{2}g{t^2} = \frac{1}{2}{.10.5^2} = 125m\)
Một vật được ném ngang ở độ cao \(45{\rm{ }}m\) so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 10{\rm{ }}m/{s^2}\). Thời gian vật rơi tới khi chạm đất là:
Ta có, thời gian chạm đất của vật ném ngang: \(t = \sqrt {\frac{{2h}}{g}} \)
Thay số, ta được: \(t = \sqrt {\frac{{2.45}}{{10}}} = 3{\rm{s}}\)
Một viên bi được ném theo phương ngang với vận tốc \(2{\rm{ }}m/s\) từ độ cao \(5{\rm{ }}m\) so với mặt đất. Lấy \(g = 10{\rm{ }}m/{s^2}\). Tầm ném xa của viên bi là:
Ta có, tầm xa của vật ném ngang: \(L = {v_0}\sqrt {\frac{{2h}}{g}} = 2\sqrt {\frac{{2.5}}{{10}}} = 2m\)
Một vật được ném theo phương ngang với tốc độ \({v_0} = 10m/s\) từ độ cao h so với mặt đất. Chọn hệ trục tọa độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều vận tốc đầu, Oy hướng thẳng đứng xuống dưới. Gốc thời gian là lúc ném. Lấy \(g = 10m/{s^2}\). Phương trình quỹ đạo của vật là:
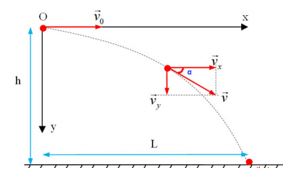
Phương trình chuyển động:
+ Theo phương Ox: \(x = {v_0}t\) (1)
+ Theo phương Oy: \(y = \dfrac{1}{2}g{t^2}\) (2)
Phương trình quỹ đạo (thay t ở (1) vào (2)): \(y = \dfrac{g}{{2v_0^2}}{x^2}\)
=> phương trình quỹ đạo của vật ném ngang trong trường hợp trên: \(y = \dfrac{g}{{2v_0^2}}{x^2} = \dfrac{{10}}{{{{2.10}^2}}} = 0,05{{\rm{x}}^2}\)
Một viên bi lăn theo cạnh của một mặt bàn nằm ngang cao \(1,25{\rm{ }}m\). Khi ra khỏi mép bàn nó rơi xuống nền nhà, cách mép bàn theo phương ngang \(2{\rm{ }}m\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Tốc độ của viên bi khi nó ở mép bàn là:
Ta có, tầm xa của vật: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \)
Vận tốc của vật khi ở mép bàn chính là vận tốc ban đầu:
\( \to {v_0} = \frac{L}{{\sqrt {\frac{{2h}}{g}} }} = \frac{2}{{\sqrt {\frac{{2.1,25}}{{10}}} }} = 4m/s\)
Một máy bay trực thăng cứu trợ bay với vận tốc không đổi \({v_0}\) theo phương ngang ở độ cao \(1500{\rm{ }}m\) so với mặt đất. Máy bay chỉ có thể tiếp cận được khu vực cách điểm cứu trợ \(2{\rm{ }}km\) theo phương ngang. Lấy \(g = 9,8{\rm{ }}m/{s^2}\). Để hàng cứu trợ thả từ máy bay tới được điểm cần cứu trợ thì máy bay phải bay với vận tốc bằng:
Ta có, tầm xa của vật: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \)
\( \to {v_0} = \frac{L}{{\sqrt {\frac{{2h}}{g}} }} = \frac{2}{{\sqrt {\frac{{2.1500}}{{9,8}}} }} = 114,31m/s\)
Một vật được ném ngang từ độ cao \(h\) ở nơi có gia tốc rơi tự do là \(g = 10{\rm{ }}m/{s^2}\) với vận tốc ban đầu \({v_0}\). Biết sau \(2s\), véctơ vận tốc của vật hợp với phương ngang góc \({30^0}\). Tốc độ ban đầu của vật gần nhất giá trị nào sau đây?
+ Vận tốc của vật theo các phương :
- Theo phương Ox: \({v_x} = {v_0}\)
- Theo phương Oy: \({v_y} = gt\)
+ Theo đầu bài, ta có:
\(\begin{array}{l}\tan \alpha = \frac{{{v_y}}}{{{v_x}}} \leftrightarrow \tan {30^0} = \frac{{gt}}{{{v_0}}}\\ \to {v_0} = \frac{{gt}}{{\tan {{30}^0}}} = \frac{{10.2}}{{\frac{1}{{\sqrt 3 }}}} = 20\sqrt 3 \left( {m/s} \right)\end{array}\)
Một quả cầu được ném theo phương ngang từ độ cao 80 m. Sau khi chuyển động 3s, vận tốc của quả cầu hợp với phương ngang góc 450. Vận tốc ban đầu của quả cầu và vận tốc chạm đất của quả cầu là:
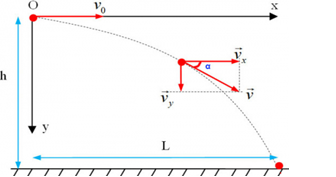
+ Góc hợp bởi vecto vận tốc của vật và phương ngang là:\(\alpha = \left( {\overrightarrow v ;\overrightarrow {{v_x}} } \right) = {45^0}\)
Ta có: \(\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}} = \dfrac{{gt}}{{{v_0}}} \Leftrightarrow \tan 45 = \dfrac{{10.3}}{{{v_0}}} \Rightarrow {v_0} = 30m/s\)
+ Vận tốc chạm đất: \({v_{cd}} = \sqrt {v_0^2 + 2gh} = \sqrt {{{30}^2} + 2.10.80} = 50m/s\)
