Đơn vị không phải đơn vị của công suất là
A, B, D - đúng
C - không phải là đơn vị của công suất đơn vị của công suất là \(J/s\)
Một động cơ điện cung cấp công suất $15 kW$ cho một cần cẩu nâng $1000 kg$ lên cao $30 m$. Lấy $g = 10 m/s^2$. Thời gian tối thiểu để thực hiện công việc đó là:
Ta có:
+ Công \(A = Fs\cos \alpha = P.h = mgh\)
+ Công suất: \(P = \dfrac{A}{t} \to t = \dfrac{A}{P}\)
=> Thời gian tối thiểu để thực hiện công việc đó là: \(t = \dfrac{A}{P} = \dfrac{{mgh}}{P} = \dfrac{{1000.10.30}}{{{{15.10}^3}}} = 20s\)
Một xe tải chạy đều trên đường ngang với tốc độ \(54 km/h\). Khi đến quãng đường dốc, lực cản tác dụng lên xe tăng gấp ba nhưng công suất của động cơ chỉ tăng lên được hai lần. Tốc độ chuyển động đều của xe trên đường dốc là:
Do xe chạy đều nên \(F = F_c\)
\(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{F_1}{v_1}}}{{{F_2}{v_2}}} = > {v_2} = \dfrac{{{P_2}{F_1}{v_1}}}{{{P_1}{F_2}}}\)
Theo đề bài \({F_2} = 3{F_1};\,{P_2} = 2{P_1} = > {v_2} = 10\,m/s\)
Một máy bay khối lượng 3000kg khi cất cánh phải mất 80s để bay lên tới độ cao 1500m. Lấy g = 9,8m/s2. Xác định công suất của động cơ máy bay. Cho rằng công mà động cơ máy bay sinh ra lúc này chủ yếu là để nâng máy bay lên cao.
Lực nâng máy bay lên cao phải có độ lớn bằng trọng lượng của máy bay :
\(F = P = mg = 3000.9,8 = 29400{\rm{ }}N\)
Do đó, động cợ máy bay phải thực hiện công :
\(A = F.h = 29400.1500 = 44,{1.10^6}{\rm{ }}J\)
Suy ra công suất của động cơ máy bay :
\({P_{dc}} = \dfrac{A}{t} = \dfrac{{44,{{1.10}^6}}}{{80}} = 551,25\left( {kW} \right)\)
Một cần cẩu nâng một vật có khối lượng 2 tấn làm cho vật chuyển động nhanh dần đều theo phương thẳng đứng lên cao \(12,5m\) với gia tốc \(1m/{s^.}^2\). Lấy \(g = 10m/{s^2}\). Hãy tính công mà cần cầu thực hiện và công suất trung bình của cần cẩu ấy.
Ta có: \(\left\{ \begin{array}{l}m = 2T = 2000kg\\s = h = 12,5m\\a = 1m/{s^2}\\g = 10m/{s^2}\end{array} \right.\)
Biểu diễn các lực tác dụng vào thang máy trên hình:
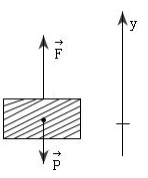
Áp dụng định luật II Niuton ta có: \(\overrightarrow F + \overrightarrow P = m.\overrightarrow a \,\,\left( * \right)\)
Chiếu (*) lên Oy ta có:
\(\begin{array}{l}F - P = ma \Rightarrow F = P + ma = m\left( {g + a} \right)\\ \Rightarrow F = 2000.\left( {10 + 1} \right) = 22000N\end{array}\)
Công mà cần cẩu thực hiện:
\(A = F.s = 22000.12,5 = 275000J\)
Lại có quãng đường vật đi được trong 12,5m là:
\(s = {v_0}t + \dfrac{1}{2}a{t^2} \Leftrightarrow 12,5 = 0 + \dfrac{1}{2}.1.{t^2} \Rightarrow t = 5s\)
Công suất trung bình của cần cẩu:
\(P = \dfrac{A}{t} = \dfrac{{275000}}{5} = 55000W = 55kW\)
Một dây cáp sử dụng động cơ điện tạo ra một lực không đổi 50N tác dụng lên vật và kéo vật đi một đoạn đường thẳng dài 30m trong thời gian 1 phút. Công suất của động cơ là:
Áp dụng công thức: \({\rm P} = \dfrac{A}{t}\)
\( \Rightarrow {\rm P} = \dfrac{A}{t} = \dfrac{{F.s}}{t} = \dfrac{{50.30}}{{60}} = 25({\rm{W}})\)
Một người đàn kéo một khối gỗ với môt lực 100N đi một đoạn đường 30m trong 3 phút. Biết lực kéo và phương dịch chuyển song song với nhau. Tìm công suất của người này khi kéo khối gỗ.
Áp dụng công thức: \({\rm P} = \dfrac{A}{t}\)
\( \Rightarrow {\rm P} = \dfrac{A}{t} = \dfrac{{F.s}}{t} = \dfrac{{100.30}}{{180}} = 16,67({\rm{W}})\)
Một bóng đèn sợi đốt có công suất 100W tiêu thụ năng lượng 1000J. Thời gian thắp sáng bóng đèn đó là?
Áp dụng công thức: \({\rm P} = \dfrac{A}{t}\)
\( \Rightarrow t = \dfrac{P}{A} = \dfrac{{1000}}{{100}} = 10(s)\)
Trên công trường xây dựng, người thợ sử động cơ điện để kéo một khối gạch nặng 85kg lên độ cao 10,7m trong thời gian 23,2s. Giải thiết cho khối gạch chuyển động đều. Công suất tối thiểu của động cơ gần nhất với giá trị nào sau đây. Lấy g = 9,8 m/s2.
Áp dụng công thức: \({\rm P} = \dfrac{A}{t}\)
\( \Leftrightarrow {\rm P} = \dfrac{{F.s}}{t} = \dfrac{{P.s}}{t} = \dfrac{{m.g.s}}{t}\)
\( \Leftrightarrow {\rm P} = \dfrac{{85.9,8.10,7}}{{23,2}}\)
\( \Rightarrow {\rm P} \approx 384{\rm{W}}\)
Tính công suất của động cơ máy bay biết rằng nó đang bay với tốc độ 250 m/s và động cơ sinh ra lực kéo 2.106N để duy trì tốc độ đó.
Áp dụng công thức: \({\rm P} = \dfrac{A}{t}\)
\( \Leftrightarrow {\rm P} = \dfrac{{F.s}}{t} = F.v\)
\( \Rightarrow {\rm P} = {2.10^6}.250 = {5.10^8}{\rm{W}}\)

