Ôn tập chủ đề 1: Mô tả chuyển động

Chuyển động cơ là sự dời chỗ của vật theo thời gian

Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.

Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ  đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

Véctơ vận tốc trung bình của vật được xác định bởi biểu thức: $\overrightarrow {{v_{tb}}}  = \frac{{\Delta \overrightarrow x }}{{\Delta t}}$

A- quỹ đạo của hòn đá có dạng cong

B- đường từ Hà Nội - TP. HCM có nhiều khúc quanh co, ngoằn nghèo => quỹ đạo của xe oto không phải là đường thẳng

C- quỹ đạo của viên bi là một đường thẳng

D- quỹ đạo của tờ giấy là đường cong, ngoằn nghèo

Do: Chọn gốc tọa độ không trùng với vị trí ban đầu, gốc thời gian trùng với thời điểm ban đầu

=> phương trình chuyển động của chất điểm: $x = {x_0} + vt$

Khi đứng ở Trái Đất, ta sẽ thấy

+ Trái Đất đứng yên

+ Mặt Trăng và Mặt Trời quay quanh Trái Đất

Để xác định hành trình của một con tàu trên biển, người ta dùng kinh độ, vĩ độ cùng hướng đi của tàu tại điểm đó mà không dùng đến thông tin ngày - giờ con tàu đến điểm đó.

Trong các trường hợp trên, thời điểm mà ta xét trùng với số đo khoảng thời gian trôi là: Một đoàn tàu xuất phát từ Vinh lúc $0$ giờ, đến $8$ giờ $05$ phút thì đoàn tàu đến Huế.

Ta có, Một ôtô chở khách chạy trên đường.

Khi nói ôtô đang đứng yên thì vật mốc là hành khách

A, C, D - đúng

B- sai vì:

+ Tại thời điểm $t_0$ vật có tọa độ $x_1=x_0$

+ Tại thời điểm $t$ vật có tọa độ $x_2=x_0+v(t-t_0)$

=> Độ dời từ thời điểm t₀ tới thời điểm t là $\Delta x = x_2 -x_1 =v(t - {t_0})$

Ta có:

+ Thuyền (1)

+ Dòng nước (2)

+ Bờ sông (3)

+ Vận tốc của thuyền (1) so với dòng nước (2): ${v_{12}} = 15km/h$

+ Vận tốc của dòng nước (2) so với bờ (3): ${v_{23}}$

+ Vận tốc của thuyền (1) so với bờ (2): ${v_{13}}$

- Khi thuyền đi xuôi dòng: ${v_{13}} = {v_{12}} + {v_{23}}$

Khi thuyền đi ngược dòng: $v{'_{13}} = {v_{12}} - {v_{23}}$

- Gọi ${t_1},{t_2}$ lần lượt là thời gian đi và về của thuyền, ta có:

$\left\{ \begin{array}{l}{t_1} = \frac{{AB}}{{{v_{13}}}} = \frac{{AB}}{{{v_{12}} + {v_{23}}}}\\{t_2} = \frac{{AB}}{{v{'_{13}}}} = \frac{{AB}}{{{v_{12}} - {v_{23}}}}\end{array} \right.$  

Theo đầu bài, ta có:

 $\begin{array}{l}{t_1} + {t_2} = 9 \to \frac{{AB}}{{{v_{12}} + {v_{23}}}} + \frac{{AB}}{{{v_{12}} - {v_{23}}}} = 9\\ \leftrightarrow \frac{{60}}{{15 + {v_{23}}}} + \frac{{60}}{{15 - {v_{23}}}} = 9\\ \leftrightarrow 60\left( {15 - {v_{23}}} \right) + 60\left( {15 + {v_{23}}} \right) = 9\left( {{{15}^2} - v_{23}^2} \right)\\ \to {v_{23}} = 5km/h\end{array}$

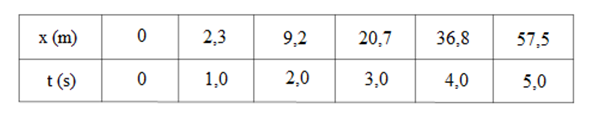
Ta có: Vận tốc trung bình: ${v_{tb}} = \frac{{\Delta x}}{{\Delta t}}$

Trong 3s cuối, oto có:

       + Độ dời: $\Delta x = 57,5 - 9,2 = 48,3m$

       + Khoảng thời gian: $\Delta t = 3{\rm{s}}$

$\to {v_{tb}} = \frac{{\Delta x}}{{\Delta t}} = \frac{{48,3}}{3} = 16,1(m/s)$

Ta có:

+ Thuyền (1)

+ Dòng nước (2)

+ Bờ sông (3)

+ Vận tốc của thuyền (1) so với dòng nước (2): ${v_{12}}$

+ Vận tốc của dòng nước (2) so với bờ (3): ${v_{23}}$

+ Vận tốc của thuyền (1) so với bờ (2): ${v_{13}}$

- Khi xuôi dòng: $v{'_{13}} = {v_{12}} + {v_{23}}$

Khi thuyền ngược dòng: ${v_{13}} = {v_{12}} - {v_{23}}$

- Gọi ${t_1},{t_2}$ lần lượt là thời gian đi xuôi dòng và đi ngược dòng của thuyền, ta có:

$\left\{ \begin{array}{l}{t_1} = \frac{{AB}}{{{v_{13}}}} = \frac{{AB}}{{{v_{12}} + {v_{23}}}} = 2{\rm{       }}\left( 1 \right)\\{t_2} = \frac{{AB}}{{v{'_{13}}}} = \frac{{AB}}{{{v_{12}} - {v_{23}}}} = 3{\rm{       }}\left( 2 \right)\end{array} \right.$

Từ (1) và (2), ta suy ra:

$\begin{array}{l}2{v_{12}} + 2{v_{23}} = 3{v_{12}} - 3{v_{23}}\\ \to {v_{12}} = 5{v_{23}} = 5.5 = 25km/h\end{array}$

Thế vào (1), ta được: $AB = 2\left( {{v_{12}} + {v_{23}}} \right) = 2\left( {25 + 5} \right) = 60km$

Các nhận xét đúng là:

+ Va li đứng yên so với thành toa.

+ Va li chuyển động so với đường ray.

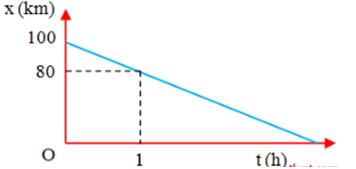
Phương trình chuyển động: $x = {x_0} + vt$

Từ đồ thị x-t, ta có:

+ Tại thời điểm ${t_0} = 0$ : ${x_0} = 100km$

+ Tại $t = 1h$: $x = 80km = {x_0} + v.1 \to v = \frac{{80 - 100}}{1} =  - 20(km/h)$

=> phương trình chuyển động của vật: $x = 100 - 20t{\rm{      }}(km)$

Người lái đò đang ngồi yên trên chiếc thuyền thả trôi theo dòng nước thì Người lái đò đứng yên so với thuyền và dòng nước

Vì khoảng cách giữa người đó với dòng nước không thay đổi

Ta có: $\left\{ \begin{array}{l}{v_{tb}} = \dfrac{{{s_1}}}{{{t_1}}} = \dfrac{9}{1} = 9km/h\\{v_{nb}} = \dfrac{{{s_2}}}{{{t_2}}} = \dfrac{{50}}{{60}} = \dfrac{5}{6}m/s = 3km/h\end{array} \right.$

Ta có: $\overrightarrow {{v_{tb}}}  = \overrightarrow {{v_{tn}}}  + \overrightarrow {{v_{nb}}}$

Do thuyền chạy ngược dòng sông nên:

${v_{tb}} = {v_{tn}} - {v_{nb}} \Rightarrow {v_{tn}} = {v_{tb}} + {v_{nb}} = 9 + 3 = 12km/h$

Tàu S1 xuất phát lúc 19h00min ngày 8 tháng 3 đếnn 4h00min ngày 10 tháng 3 sẽ chạy mất:

$t=33h00\min$

Thời gian tàu phải nghỉ ở một số ga để trả khách:

${{t}_{tra\,khach\,}}=39\min$

Khoảng thời gian tàu chạy là:

$\Delta t=33h00min39min=32h21min$

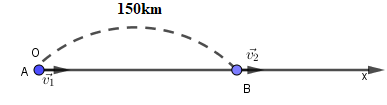
Chọn gốc tọa độ tại A, chiều dương chọn là chiều từ A hướng B. Chọn gốc thời gian là lúc 14h

Giả sử phương trình chuyển động của ô tô qua A có dạng:

${x_A} = {x_{0A}} + {v_A}\left( {t - {t_{0A}}} \right)$

Với: $\left\{ \begin{array}{l}{x_{0A}} = 0\\{t_{0A}} = 0\\{v_A} = 75km/h\end{array} \right. \Rightarrow {x_A} = 0 + 75\left( {t - 0} \right) = 75t\,\,\left( {km} \right)$

Giả sử phương trình chuyển động của ô tô qua B có dạng:

${x_B} = {x_{0B}} + {v_B}\left( {t - {t_{0B}}} \right)$

Với: $\left\{ \begin{array}{l}{x_{0B}} = 150km\\{t_{0B}} = 0\\{v_B} = 50km/h\end{array} \right. \Rightarrow {x_B} = 150 + 50t\,\,\left( {km} \right)$

Hai xe gặp nhau khi: ${x_A} = {x_B} \Rightarrow 75t = 150 + 50t \Rightarrow t = 6h$

Thay t = 6h vào phương trình ta có: ${x_A} = 75.6 = 450\left( {km} \right)$

Vị trí hai xe gặp nhau cách B: $d = 450 - 150 = 300\left( {km} \right)$