Chuyển động tròn

Chuyển động tròn là chuyển động có quỹ đạo là một đường tròn

Lực hướng tâm: \({F_{ht}} = m{a_{ht}} = \dfrac{{m{v^2}}}{r} = m.{\omega ^2}r\)

Ta có:

Chuyển động tròn đều là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.

=> Chuyển động quay của kim phút trên mặt đồng hồ chạy đúng giờ là chuyển động tròn đều

Ta có: Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

=> Các phương án:

A - sai vì vật có thể chịu tác dụng của nhiều lực

B - đúng

C - sai vì lực hướng tâm không phải là lực mới

D - sai vì hợp lực của tất cả các lực tác dụng lên vật hướng vào tâm

Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.

A, B, D - đúng

C - sai vì: \({a_{ht}} = \dfrac{{{v^2}}}{r} = {\omega ^2}r\)

Có lực hướng tâm khi vật chuyển động cong

Ta có, lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\frac{{{v^2}}}{r}\)

Thay số ta được: \({F_{ht}} = 0,15\frac{{{2^2}}}{{1,5}} = 0,4N\)

+ Tần số: \(f = \frac{{120}}{{60}} = 2\left( {H{\rm{z}}} \right)\)

+ Tốc độ góc: \(\omega  = 2\pi f = 2\pi .2 = 4\pi \left( {ra{\rm{d}}/s} \right)\)

+ Ta có, lực hướng tâm: \({F_{ht}} = m{\omega ^2}r = 0,25{\left( {4\pi } \right)^2}1,2 \approx 47,3N\)

Ta có:

+ Hợp lực tác dụng lên ô tô: \(\overrightarrow F  = \overrightarrow P  + \overrightarrow N \)

+ Chiếu lên phương hướng tâm, ta được:

\(\begin{array}{l}{F_{ht}} = Pc{\rm{os3}}{{\rm{0}}^0} - N = m\frac{{{v^2}}}{r}\\ \to N = Pc{\rm{os3}}{{\rm{0}}^0} - m\frac{{{v^2}}}{r} = mgc{\rm{os3}}{{\rm{0}}^0} - m\frac{{{v^2}}}{r}\\ = 2500.10.c{\rm{os3}}{{\rm{0}}^0} - 2500\frac{{{{15}^2}}}{{1000}} = 21088N\end{array}\)

Ta có:

+ Chu kì của chuyển động: \(T = 90.60 = 5400{\rm{s}}\)

+ Tốc độ góc: \(\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{5400}}\left( {ra{\rm{d}}/s} \right)\)

+ Vận tốc dài: \(v = \omega r = \frac{{2\pi }}{{5400}}.\left( {6380 + 320} \right).1000 = 7795,8\left( {m/s} \right)\)

Ta có:

+ Tốc độ góc: \(\omega  = \frac{{2\pi }}{T}\)

+ Lực hướng tâm: \({F_{ht}} = m\frac{{{v^2}}}{r} = m{\omega ^2}r\)

=> Ta suy ra:

Độ lớn lực hướng tâm tác dụng lên vệ tinh:

\({F_{ht}} = m{\omega ^2}r = \frac{{m4{\pi ^2}(R + h)}}{{{T^2}}} = \frac{{100.4.{\pi ^2}.6553.1000}}{{{{({{5.10}^3})}^2}}} \approx 1035{\rm{ N}}\)

Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.

Khi đó:

\({F_{hd}} = {F_{ht}} = m\frac{{{v^2}}}{r}\)

Với: \(r = R + h\) và \(v = \omega r = \frac{{2\pi }}{T}(R + h)\)

\( \Rightarrow {F_{hd}} = {F_{ht}} = m{\omega ^2}r = \frac{{m4{\pi ^2}(R + h)}}{{{T^2}}} = \frac{{20.4{\pi ^2}.7400.1000}}{{{{86400}^2}}} \approx 0,783{\rm{ N}}\)

Từ đầu bài ta có: Tốc độ góc \(\omega  = 60\) vòng/phút \( = 60.\frac{{2\pi }}{{60}} = 2\pi \left( {ra{\rm{d}}/s} \right)\)

Mặt khác: \(\omega  = \frac{{2\pi }}{T}\)

Ta suy ra chu kì của hòn đá (thời gian hòn đá quay hết một vòng) \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)

+ Ta có:

- Chu kì của kim giờ: \({T_g} = 12g = 12.60 = 720ph\)

- Chu kì của kim phút: \({T_{ph}} = 60ph\)

+ Vận tốc dài: \(v = \omega r = \frac{{2\pi }}{T}r\)

Ta suy ra, tỉ số: \(\dfrac{{{v_{ph}}}}{{{v_g}}} = \dfrac{{\dfrac{{2\pi {r_{ph}}}}{{{T_{ph}}}}}}{{\dfrac{{2\pi {r_g}}}{{{T_g}}}}} = \dfrac{{{r_{ph}}{T_g}}}{{{r_g}{T_{ph}}}} = \dfrac{{4.720}}{{3.60}} = 16\)

Ta có:

Vận tốc dài: \(v = 40km/h = \frac{{100}}{9}m/s\)

Gia tốc hướng tâm của xe: \({a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{{\left( {\frac{{100}}{9}} \right)}^2}}}{{100}} = 1,23m/{s^2}\)

Ta có:

+ Vận tốc dài và vận tốc góc liên hệ với nhau theo biểu thức: \(v = \omega r\)  (1)

+ Gia tốc hướng tâm của vật: \({a_{ht}} = \frac{{{v^2}}}{r} = {\omega ^2}r\) (2)

Từ (1) và (2), ta suy ra: \({a_{ht}} = v\omega  = 5.10 = 50m/{s^2}\)

R₁ = 15cm; R₂ = 20cm

Chu kì của kim giờ: T₂ = 12h = 43200s

Chu kì của kim phút: T₂ = 1h = 3600s

Tốc độ góc: \(\left\{ \begin{array}{l}{\omega _1} = \dfrac{{2\pi }}{{{T_1}}} \approx 1,{454.10^{ - 4}}\,\,rad/s\\{\omega _2} = \dfrac{{2\pi }}{{{T_2}}} \approx 1,{744.10^{ - 3}}\,\,rad/s\end{array} \right.\)

Lúc 12h hai kim trùng nhau.

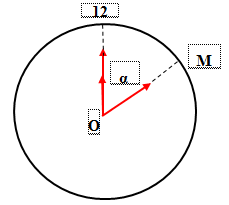
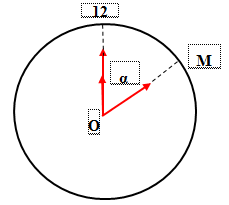
Ta có: \({\alpha _2} - {\alpha _1} = 2\pi  \Leftrightarrow {\omega _2}t - {\omega _1}t = 2\pi  \Rightarrow t = \dfrac{{2\pi }}{{{\omega _2} - {\omega _1}}} \approx 3928s \approx 1h5ph28s\)