Từ độ cao 5,0 m so với mặt đất, người ta ném một vật khối lượng 200 g thẳng đứng lên cao với vận tốc đầu là 2 m/s. Bỏ qua lực cản của không khí. Lấy g ≈ 10 m/s2. Xác định cơ năng của vật tại vị trí cao nhất mà vật đạt tới. Chọn mốc thế năng tại vị trí ném.
Chọn mốc thế năng tại vị trí ném vật
Cơ năng tại vị trí ném là:
\({{\rm{W}}_1} = {{\rm{W}}_{d1}} + {{\rm{W}}_{t1}} = \dfrac{1}{2}mv_1^2 + mg{h_1} = \dfrac{1}{2}.0,{2.2^2} + 0,2.10.0 = 1J\)
Theo định luật bảo toàn cơ năng ta có cơ năng tại vị trí cao nhất bằng với cơ năng tại vị trí ném nên ta có cơ năng tại vị trí cao nhất là 1J
Từ mặt đất ném vật nặng 500g lên cao với vận tốc ban đầu là 10m/s. Tại độ cao \(h'\) vật đặt vận tốc 6m/s. Lấy \(g = 10\left( {m/{s^2}} \right)\), chọn mốc thế năng tại mặt đất. Độ cao \(h'\) có giá trị là:
Mốc thế năng tại mặt đất.
Cơ năng của vật tại mặt đất là:
\({{\rm{W}}_1} = {{\rm{W}}_{d1}} + {{\rm{W}}_{t1}} = \dfrac{1}{2}mv_1^2 + mg{h_1} = \dfrac{1}{2}.0,{5.10^2} + 0,2.9,8.5 = 25J\)
Cơ năng tại độ cao \(h'\) là:
\({{\rm{W}}_2} = {{\rm{W}}_{d2}} + {{\rm{W}}_{t2}} = \dfrac{1}{2}mv_2^2 + mg{h_1} = \dfrac{1}{2}.0,{5.6^2} + 0,5.10.h' = 9 + 5h'\)
Theo định luật bảo toàn cơ năng ta có: \({{\rm{W}}_1} = {{\rm{W}}_2}\)
\(\begin{array}{l} \Rightarrow 9 + 4,9h' = 25\\ \Rightarrow h' = 3,2m\end{array}\)
Độ cao \(h' = 3,2m\)
Một vật khối lượng 100 g được ném thẳng đứng từ độ cao 5,0 m lên phía trên với vận tốc đầu là 10 m/s. Bỏ qua lực cản của không khí. Lấy g ≈ 10 m/s2. Xác định cơ năng của vật tại vị trí của nó sau 0,50 s kể từ khi chuyển động.
Chọn mặt đất làm gốc tính thế năng, chiều từ mặt đất lên cao là chiều dương. Trường hợp này, vật chuyển động chậm dần đều từ độ cao \({z_0}\) với gia tốc \(g\) và vận tốc đầu \({v_0}\), nên vận tốc \(v\) và độ cao \(z\) của vật sau khoảng thời gian \(t\) được tính theo các công thức chuyển động biến đổi
Vận tốc của \(v\) của vật là: \(v = gt + {v_0} = - 10.0,5 + 10 = 5m/s\)
Độ cao z của vật là: \(z = \dfrac{{g{t^2}}}{2} + {v_0}t + {z_0} = \dfrac{{ - 10.0,{5^2}}}{2} + 10.5 + 5 = 11,25\left( m \right)\)
Cơ năng tại vị trí độ cao z là: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \dfrac{1}{2}m{v^2} + mg{\rm{z}}\)
Thay số ta tìm được \({\rm{W}} \approx 12,5J\)
Một con cá heo trong khi nhào lộn đã vượt khỏi mặt biển tới độ cao 5m. Nếu coi cá heo vượt lên khỏi mặt biển được chỉ nhờ động năng nó có vào lúc rời mặt biển và lấy g = 10m/s2 thì vận tốc của cá heo vào lúc rời mặt biển là bao nhiêu? Chọn mốc thế năng tại mặt biển
Cơ năng khi cá heo mới vọt khỏi mặt biển: \({{\rm{W}}_1} = {{\rm{W}}_{d1}} + {{\rm{W}}_{t1}} = \dfrac{1}{2}m{v^2}\)
Cơ năng khi đạt tới độ cao 5m: \({{\rm{W}}_2} = {{\rm{W}}_{d2}} + {{\rm{W}}_{t2}} = mgh\)
Áp dụng định luật bảo toàn cơ năng tại thời điểm mới vượt khỏi mặt biển và khi đạt độ cao 5m ta có:
\(\dfrac{1}{2}m{v^2} = mgh\)
\( \Rightarrow \dfrac{1}{2}{v^2} = 10.5 \Rightarrow v = 10m/s\)
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h = 60m so với mặt đất. Chọn mốc tính thế năng tại mặt đất. Độ cao mà tại đó vật có động năng bằng ba lần thế năng là
Ta có \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_d}\)
mặt khác \({{\rm{W}}_d} = 3{W_t}\)
\(\begin{array}{l} \Rightarrow {\rm{W}} = {{\rm{W}}_d} + {W_t} = 4{W_t}\\ \Rightarrow mgh = 4mgh'\\ \Rightarrow h' = \dfrac{h}{4} = \dfrac{{60}}{4} = 15m\end{array}\)
Một vật khối lượng 10 kg trượt không vận tốc đầu từ đỉnh của một mặt dốc có
độ cao 20 m. Tới chân mặt dốc, vật có vận tốc 15 m/s. Lấy g = 10 m/s2. Công của lực ma sát trên mặt dốc này bằng:
Chọn mặt đất làm gốc tính thế năng (\({W_t} = 0\)), chiều chuyển động của vật trên mặt dốc là chiều dương.
Do chịu tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn.
Trong trường hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:
\({{\rm{W}}_2} - {{\rm{W}}_1} = \left( {\dfrac{1}{2}m{v^2} + mg{\rm{z}}} \right) - \left( {\dfrac{1}{2}mv_0^2 + mg{{\rm{z}}_0}} \right) = {A_{m{\rm{s}}}}\)
\( \Rightarrow {A_{m{\rm{s}}}} = \left( {\dfrac{1}{2}{{.10.15}^2} - 10.20} \right) = - 875J\)
Một vật nặng nhỏ m chuyển động từ đỉnh A có độ cao 3m theo mặt phẳng nghiêng AB, sau đó chuyển động thẳng đứng lên trên đến C có độ cao 4m. Bỏ qua mọi ma sát, lấy g = 10m/s2. Tính vận tốc ban đầu của vật tại A

Trong quá trình chuyển động từ A → B → C cơ năng của vật được bảo toàn.
Chọn mốc thế năng tại B, ta có: \(\left\{ \begin{array}{l}{z_B} = 0\\{z_A} = 3m\\{z_C} = 4m\end{array} \right.\)
Cơ năng tại C:
\(\begin{array}{l}{{\rm{W}}_C} = {{\rm{W}}_{tC}} + {{\rm{W}}_{dC}} = mg{z_C} + \dfrac{1}{2}mv_C^2 = mg{z_C} = 10.m.4\\ \Rightarrow {{\rm{W}}_C} = 40.m\,\,\left( J \right)\end{array}\)
Cơ năng tại A:
\(\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_{tA}} + {{\rm{W}}_{dA}} = mg{z_A} + \dfrac{1}{2}mv_A^2 = 10.m.3 + \dfrac{1}{2}mv_A^2\\ \Rightarrow {{\rm{W}}_A} = 30m + \dfrac{1}{2}mv_A^2\,\,\left( J \right)\end{array}\)
Cơ năng được bảo toàn nên:
\({{\rm{W}}_A} = {{\rm{W}}_C} \Leftrightarrow 30m + \dfrac{1}{2}mv_A^2\, = 40m \Leftrightarrow \dfrac{1}{2}v_A^2\, = 10 \Rightarrow {v_A} = \sqrt {20} \,m/s\)
Viên đạn khối lượng m = 100g đang bay với vận tốc v0 = 10m/s theo phương ngang đến cắm vào bao cát khối lượng M = 400g treo ở đầu sợi dây dài l = 1m đang đứng yên ở vị trí cân bằng, đầu kia của sợi dây treo vào điểm cố định. Sau khi cắm vào bao cát hệ chuyển động lên đến vị trí dây treo lệch với phương thẳng đứng một góc xấp xỉ bằng:

Chọn mốc thế năng là vị trí va chạm
- Xét thời điểm ngay khi va chạm mềm giữa viên đạn và bao cát là hệ kín
- Áp dụng định luật bảo toàn động lượng của hệ
\({m_1}\overrightarrow {{v_1}} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \)
\(\overrightarrow v \) cùng hướng với \(\overrightarrow v \)
Vận tốc của đạn và bao cát sau va chạm:
\(v = {v_{12}} = \dfrac{{{m_1}{v_1}}}{{{m_1} + {m_2}}} = \dfrac{{m{v_0}}}{{m + M}} = \dfrac{{0,1.10}}{{0,1 + 0,4}} = 2\left( {m/s} \right)\)
Cơ năng của hệ ban đầu ( trước khi va chạm):
\(\begin{array}{l}{{\rm{W}}_1} = \left( {{{\rm{W}}_{d1}} + {{\rm{W}}_{t1}}} \right) + \left( {{{\rm{W}}_{d2}} + {{\rm{W}}_{t2}}} \right)\\ = \left( {\dfrac{1}{2}{m_1}v_1^2 + 0} \right) + \left( {0 + 0} \right) = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}.0,{1.10^2} = 5J\end{array}\)
Cơ năng của hệ lúc sau ( ngay sau va chạm):
\(\begin{array}{l}{{\rm{W}}_1} = \left( {{{\rm{W}}_{d12}} + {{\rm{W}}_{t12}}} \right) + \left( {{{\rm{W}}_{d2}} + {{\rm{W}}_{t2}}} \right)\\ = \left( {\dfrac{1}{2}{m_{12}}v_{12}^2 + 0} \right) = \dfrac{1}{2}\left( {0,1 + 0,2} \right){2^2} = 1J\end{array}\)
Sau khi cắm vào bao cát hệ chuyển động lên đến vị trí dây treo lệch với phương thẳng đứng một góc lớn nhất \({\alpha _0}\) ứng với thế năng lớn nhất động năng bằng không vậy ta có:
\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_{ma{\rm{x}}}} = {m_{12}}gl\left( {1 - co{\rm{s}}{\alpha _0}} \right)\\ \Rightarrow 1 = \left( {0,1 + 0,4} \right).10.1.\left( {1 - co{\rm{s}}{\alpha _0}} \right)\\ \Rightarrow co{\rm{s}}{\alpha _0} = 0,8 \Rightarrow {\alpha _0} \approx {37^ \circ }\end{array}\)
Để xác định vận tốc của đầu đạn người ta dùng con lắc thủ đạn, gồm một hộp đựng cát khối lượng M được treo vào một sợi dây l. Khi được bắn, đầu đạn khối lượng m bay theo phương nằm ngang, cắm vào cát và nâng hộp cát lên cao thêm một đoạn h so với vị trí cân bằng.Vận tốc của đầu đạn là:
Khi viên đạn va chạm mềm vào hộp cát
\(mv = \left( {M + m} \right)u\;\left( 1 \right)\)
Khi viên đạn và hộp cát chuyển động lên cao
\(0 + (M + m)gh = \dfrac{1}{2}(M + m){u^2} + 0\)
\( = > 2{\rm{ }}\left( {M + m} \right)gh = \left( {M + m} \right){v^2}\)
Từ (1) và (2)
\( \Rightarrow v = \dfrac{{M + m}}{m}\sqrt {2gh} \)
Một viên đạn khối lượng m = 10g bắn đi theo phương ngang với vận tốc v0 va chạm mềm với khối gỗ khối lượng M = 1kg treo đầu sợi dây nhẹ cân bằng thẳng đứng. Sau va chạm khối gỗ chứa đạn nâng lên độ cao cực đại h = 0,8m so với vị trí cân bằng ban đầu, lấy g = 9,8m/s2. Vận tốc v0 và độ cao h có giá trị:

Chọn mốc thế năng ở vị trí sợi dây thẳng đứng
Gọi vận tốc của khối gỗ và viên đạn ngay sau va chạm mền là V
Áp dụng định luật bảo toàn động lượng ta có:
\(V(M + m) = {v_0}m\left( * \right)\)
Áp dụng định luật bảo toàn cơ năng tại vị trí ban đầu và tại vị trí cực đại ta có:
\(\dfrac{{\left( {m + M} \right){V^2}}}{2} = \left( {m + M} \right)g.h\)
\( \Rightarrow V = \sqrt {2gh} = \sqrt {2.9,8.0,8} \approx 4m/s\)
\({v_0} = \dfrac{{V\left( {m + M} \right)}}{m} = 400\left( {m/s} \right)\)
Một vận động viên nặng 650N nhảy với vận tốc ban đầu \({v_0} = 2m/s\) từ cầu nhảy ở độ cao 10m xuống nước theo hướng thẳng đứng xuống dưới. Lấy \(g = 10m/{s^2}\), sau khi chạm nước người đó chuyển động thêm một độ dời 3m trong nước theo phương thẳng đứng thì dừng. Độ biến thiên cơ năng của người đó là:
Chọn gốc thế năng tại mặt nước
Khối lượng của người:
\(m = \dfrac{P}{m} = \dfrac{{650}}{{10}} = 65(kg)\)
Cơ năng ban đầu của vận động viên: \({\rm{W}} = {{\rm{W}}_{{d_0}}} + {{\rm{W}}_{{t_0}}}\)
\(\begin{array}{l} \Rightarrow {\rm{W}} = \dfrac{1}{2}mv_0^2 + mgh\\ \Rightarrow {\rm{W}} = \dfrac{1}{2}{.65.2^2} + 65.10.10\\ \Rightarrow {\rm{W}} = 6630J\end{array}\)
Cơ năng của người khi dừng lại trong nước: \({\rm{W}}' = {{\rm{W}}_t} = mg{\rm{z}} = 65.10( - 3) = - 1950J\)
Độ biến thiên cơ năng của người đó: \(\Delta W = W' - W = - 1950 - 6630 = - 8580\;(J)\)
Tính lực cản của đất khi thả rơi một hòn đá có khối lượng 500g từ độ cao 50m. Cho biết hòn đá lún vào đất một đoạn 10cm. Lấy g = 10m/s2. Bỏ qua sức cản của không khí.
Đổi 10cm = 0,1m
Khi bị lún xuống đất, cơ năng của hòn đá bằng 0.
Áp dụng định luật biến thiên cơ năng ta có:
\({A_C} = \Delta W\)
\( \Leftrightarrow - {F_C}.s = 0 - mg{h_0}\)
\(\begin{array}{l} \Leftrightarrow {F_C} = \dfrac{{mg{h_0}}}{s}\\ \Leftrightarrow {F_C} = \dfrac{{0.5.10.50}}{{0,1}}\\ \Leftrightarrow {F_C} = 2500N\end{array}\)
Khi con lắc đơn dao động từ vị trí cân bằng đến vị trí cao nhất:
Ta có \({\rm{W = }}{{\rm{W}}_d} + {{\rm{W}}_t}\)
Đồng thời cơ năng được bảo toàn \({\rm{W}} = {\rm{W}}'\)
khi con lắc đến vị trí cao nhất thì \(h = {h_{ma{\rm{x}}}}\)\( \Rightarrow {{\rm{W}}_{tmax}}\)
Hay thế năng của vật tăng dần
Một con lắc đơn gồm vật nặng \(m = 400g\), dây treo không dãn có chiều dài \(l = 1,5m\). Chọn mốc thế năng tại vị trí cân bằng của vật, lấy \(g = 10m/{s^2}\), ở góc lệch \(\alpha = {60^0}\) so với phương thẳng đứng vật có thế năng \({{\rm{W}}_t}\). Cơ năng của vật có giá trị:
- Chọn mốc tính thế năng tại vị trí thấp nhất của vật
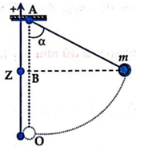
Thế năng của vật là: \({{\rm{W}}_t} = mg{\rm{z}}\)
Từ hình ta có: \(z = OB = OA - AB = l - lco{\rm{s}}\alpha = l\left( {1 - co{\rm{s}}\alpha } \right)\)
Từ đó cơ năng của vật tại vị trí ứng với \(\alpha = {60^0}\) là:
\(\begin{array}{l}{{\rm{W}}_t} = mg{\rm{z = mgl}}\left( {1 - co{\rm{s}}\alpha } \right)\\ \Rightarrow {{\rm{W}}_t} = 0.4.10.1,5.\left( {1 - co{\rm{s}}{{60}^ \circ }} \right) = 3J\end{array}\)
Khi con lắc đơn đến vị trí cao nhất thì
Ta có cơ năng bằng tổng động năng và thế năng
Theo định luật bảo toàn cơ năng ta có khi con lắc đạt độ cao cực đại tức là \(h = {h_{ma{\rm{x}}}} \Rightarrow {{\rm{W}}_{tma{\rm{x}}}}\)
Một vật có khối lượng 1 kg rơi tự do từ độ cao h = 50m xuống đất, lấy g = 10 m/s2. Động năng của vật ngay trước khi chạm đất là:
Chọn mốc thế năng tại mặt đất
Khi vật tại độ cao 50m thì cơ năng bằng thế năng của vật:
\({\rm{W = }}{{\rm{W}}_t} = mgh = 1.10.50 = 500J\)
Ngay trước khi vật chạm đất cơ năng của vật chính bằng động năng của vật
\( \Leftrightarrow {{\rm{W}}_d} = 500J\)

