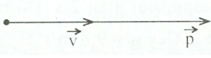
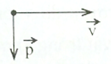
Hình nào biểu diễn đúng quan hệ giữa \(\overrightarrow v \) và \(\overrightarrow p \) của một chất điểm?
Ta có: \(\overrightarrow p = m\overrightarrow v \)
\( \to \overrightarrow p \uparrow \uparrow \overrightarrow v \)
Một vật khối lượng \(500{\rm{ }}g\) chuyển động thẳng dọc trục Ox với vận tốc \(18{\rm{ }}km/h\). Động lượng của vật bằng:
Ta có: \(18km/h = 5m/s\)
Động lượng của vật: \(\overrightarrow p = m\overrightarrow v \)
Xét về độ lớn: \(p = mv = 0,5.5 = 2,5kg.m/s\)
Trong quá trình nào sau đây, động lượng của vật không thay đổi?
Động lượng của vật: \(\overrightarrow p = m\overrightarrow v \)
Động lượng của một vật không đổi nếu \(\overrightarrow v \) không đổi.
Chất điểm M chuyển động không vận tốc đầu dưới tác dụng của lực không đổi \(\overrightarrow F \).Động lượng chất điểm ở thời điểm t là:
Ta có: Độ biến thiên động lượng của một vật trong một khoảng thời gian nào đó bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
\(\overrightarrow {{p_2}} - \overrightarrow {{p_1}} = \Delta \overrightarrow p = \overrightarrow F \Delta t\)
Ta có: Do vật chuyển động không vận tốc đầu nên:
\(\begin{array}{l}\Delta \overrightarrow p = \overrightarrow {{p_2}} = \overrightarrow p = \overrightarrow F t\\ \to \overrightarrow p = \overrightarrow F t\end{array}\)
Trên hình là đồ thị tọa độ – thời gian của một vật có khối lượng \(3 kg\). Động lượng của vật tại thời điểm \(t_1= 1s\) và thời điểm \(t_2= 5 s\) lần lượt bằng:
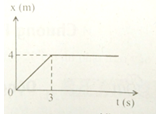
Thời điểm t = 0 đến thời điểm t = 3 s, vật chuyển động thẳng đều với vận tốc bằng 4/3 m/s.
Từ thời điểm t = 3 s vật không chuyển động.
=> Tại thời điểm t1 = 1 s ⇒ p1 = mv1 = 4 kg.m/s.
=> Tại thời điểm t2 = 5 s ⇒ p2 = mv2 = 0 kg.m/s.
Một vật \(3 kg\) rơi tự do rơi xuống đất trong khoảng thời gian \(2 s\). Độ biến thiên động lượng của vật trong khoảng thời gian đó là (lấy \(g = 9,8 m/s^2\)).
Xung lượng của trọng lực bằng độ biến thiên động lượng của vật:
\( \Rightarrow \Delta p = F.\Delta t\)
Ta có: \(F\) - ở đây chính là trọng lượng của vật \(P = mg\)
\( \Rightarrow \Delta p = P.\Delta t = mg.\Delta t = 3.9,8.2 = 58,8kg.m/s\)
Một quả bóng khối lượng 250 g bay tới đập vuông góc vào tường với tốc độ v1 = 5 m/s và bật ngược trở lại với tốc độ v2 = 3 m/s. Động lượng của vật đã thay đổi một lượng bằng
Chọn chiều dương là chiều chuyển động lúc sau của quả bóng.
Ta có: \(\Delta \overrightarrow p = m{\overrightarrow v _2} - m\overrightarrow {{v_1}} \) .
Do \({\overrightarrow v _2} \uparrow \downarrow {\overrightarrow v _1} = > \Delta p = mv_2 - m(-v_1)= m\left( {{v_2} + {v_1}} \right) = 2\,kg.m/s\)
Một vật có khối lượng $m$ chuyển động với vận tốc $3 m/s$ đến va chạm với một vật có khối lượng $2m$ đang đứng yên. Coi va chạm giữa hai vật là mềm. Sau va chạm, hai vật dính nhau và chuyển động với cùng vận tốc
Hệ hai vật ngay khi va chạm mềm là một hệ kín nên động lượng của hệ được bảo toàn:
\({m_1}{\overrightarrow v _1} + {m_2}{\overrightarrow v _2} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \)
Do \({v_2} = 0 = > v = \frac{{{m_1}{v_1}}}{{{m_1} + {m_2}}} = \frac{{m.3}}{{m + 2m}} = 1\,m/s\)
Một khẩu đại bác có khối lượng 4 tấn, bắn đi một viên đạn theo phương ngang có khối lượng 10 kg với vận tốc 400 m/s. Coi như lúc đầu hệ đại bác và đạn đứng yên. Vận tốc giật lùi của đại bác là:
Chọn chiều dương là chiều chuyển động của viên đạn.
Áp dụng định luật bảo toàn động lượng cho hệ vật:
\(\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \)
Ban đầu hệ đứng yên nên: \(\overrightarrow {{p_{tr}}} = 0\)
Ta có:
\(\begin{array}{l}
\overrightarrow {{p_{tr}}} = \overrightarrow {{p_s}} \Leftrightarrow 0 = m.\overrightarrow v + M.\overrightarrow V \\
\Rightarrow 0 = m.v - M.V \Leftrightarrow mv = M.V \Rightarrow V = \frac{{m.v}}{M} = \frac{{10.400}}{{4000}} = 1\left( {m/s} \right)
\end{array}\)
Đơn vị của động lượng là:
Biểu thức động lượng \(\overrightarrow p = m.\overrightarrow v \)
Khối lượng m đơn vị là kg, vận tốc v đơn vị là m/s
\( \Rightarrow \) Động lượng \(\overrightarrow p \) có đơn vị là \(kg.m/s\)
