Biểu thức nào sau đây xác định thế năng hấp dẫn của một vật có khối lượng m, ở độ cao h so với mặt đất. Chọn gốc thế năng ở mặt đất
Nếu chọn gốc thế năng là mặt đất thì công thức tính thế năng trọng trường của một vật ở độ cao h là:
\({{\rm{W}}_t} = mgh\)
Trong quá trình rơi tự do của một vật thì:
Trong quá trình rơi tự do của một vật thì: Động năng tăng, thế năng giảm.
Động năng là đại lượng:
Ta có biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
=> Động năng là đại lượng vô hướng, luôn dương hoặc bằng không
Một vật được ném thẳng đứng từ dưới lên cao. Trong quá trình chuyển động của vật thì:
Ta có :
Khi một vật được ném lên, độ cao của vật tăng dần nên thế năng tăng.
Trong quá trình chuyển động của vật từ dưới lên, trọng lực luôn hướng ngược chiều chuyển động nên nó là lực cản, do đó trọng lực sinh công âm.
Một ô tô khối lượng m đang chuyển động với vận tốc \(\vec v\)thì tài xế tắt máy. Công của lực ma sát tác dụng lên xe làm xe dừng lại là:
Động năng của ô tô trước khi tắt máy là: ${W_d} = \frac{{m{v^2}}}{2}$
Động năng của ô tô sau khi dừng lại là: \(W{'_d} = {\text{ }}0\)
Áp dụng định lí biến thiên động năng ta có: \(A = 0 - \frac{{m{v^2}}}{2} = - \frac{{m{v^2}}}{2}\).
Thế năng hấp dẫn là đại lượng:
Ta có, thế năng hấp dẫn là đại lượng vô hướng, có thể âm, dương hoặc bằng 0
Một vật có khối lượng m = 400 g và động năng 20 J. Khi đó vận tốc của vật là:
Từ công thức tính động năng ta có:
\({W_d} = \frac{1}{2}m{v^2} \Rightarrow v = \sqrt {\frac{{2.{W_d}}}{m}} = \sqrt {\frac{{2.20}}{{0,4}}} = 10m/s = 36km/h\)
Một người và xe máy có khối lượng tổng cộng là \(300 kg\) đang đi với vận tốc \(36 km/h\) thì nhìn thấy một cái hố cách \(12 m\). Để không rơi xuống hố thì người đó phải dùng một lực hãm có độ lớn tối thiểu là:
Từ định lí biến thiên động năng ta có:
\(A = {W_{d2}} - {W_{d1}} \Leftrightarrow {F_h}.s = 0 - \dfrac{1}{2}m{v^2} \Rightarrow F{}_h = - \dfrac{{m{v^2}}}{{2s}}\)
\( \Rightarrow {F_h} = - \dfrac{{{{300.10}^2}}}{{2.12}} = - 1250N\)
Độ lớn của lực hãm là: \( \Rightarrow {F_h} = 1250N\) dấu (-) có nghĩa là lực cản trở chuyển động.
Một người có khối lượng $50 kg$, ngồi trên ô tô đang chuyển động với vận tốc $72 km/h$. Động năng của người đó với ô tô là:
Ta có, vận tốc của người so với ô – tô là: \(v = 0m/s\) (do người đang ngồi trên ô-tô)
=> Động năng của người so với ô-tô là: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2} = 0J\)
Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng \(m = 0,2kg\) trượt không ma sát với vận tốc ban đầu bằng 0 rơi xuống đất. Cho \(AB = 50cm\), \(BC = 100cm\), \(AD = 130cm\), \(g = 10m/{s^2}\). Bỏ qua lực cản không khí. Vận tốc của vật tại điểm B có giá trị là?
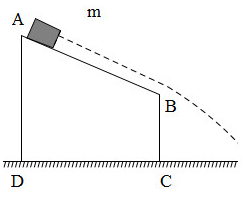
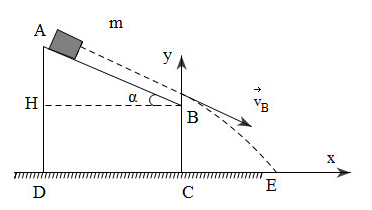
Chọn mốc thế năng tại mặt đất
Vì bỏ qua ma sát nên cơ năng của vật được bảo toàn
Ta có:
+ Cơ năng của vật tại A: ${{\rm{W}}_A} = mgAD$ (động năng của vật bằng 0 vì \({v_0} = 0\))
+ Cơ năng của vật tại B: ${{\rm{W}}_B} = \dfrac{1}{2}mv_B^2 + mgBC$
Áp dụng định luật bảo toàn cơ năng, ta có cơ năng của vật tại A bằng cơ năng của vật tại B
$\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg.AD = \dfrac{1}{2}mv_B^2 + mg.BC\\ \leftrightarrow g.AD = \dfrac{1}{2}v_B^2 + g.BC\\ \leftrightarrow 10.1,3 = \dfrac{1}{2}v_B^2 + 10.1\\ \to {v_B} = \sqrt 6 \approx 2,45m/s\end{array}$
Hai vật có khối lượng là m và $2m$ đặt ở hai độ cao lần lượt là $2h$ và $h$. Thế năng hấp dẫn của vật thứ nhất so với vật thứ hai là:
Ta có:
Thế năng của vật 1 có giá trị là: \({W_{t1}} = m.g.2.h = 2mgh\) (1).
Thế năng của vật 2 có giá trị là: \({W_{t2}} = 2.m.g.h = 2mgh\) (2).
=> Thế năng vật 1 bằng thế năng vật 2
Một thang máy có khối lượng 1 tấn chuyển động từ tầng cao nhất cách mặt đất 100m xuống tầng thứ 10 cách mặt đất 40m. Nếu chọn gốc thế năng tại tầng 10, lấy g = 9,8m/s2. Thế năng của thang máy ở tầng cao nhất là:
Ta có gốc thế năng tại tầng thứ 10 nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là: z =100 – 40 = 60m.
Thế năng của thang máy là: \({W_t} = mgz = 1000.9,8.60 = 588kJ\).
Thả một quả bóng tennit có khối lượng m = 20g từ độ cao h1 = 5m xuống mặt đất, nó nảy lên đến độ cao h2 = 3m. Lấy g = 10m/s2. Độ biến thiên cơ năng của quả tennis là
Chọn gốc thế năng tại mặt đất.
Độ biến thiên cơ năng của quả tennis là:
\({\rm{W}} = {{\rm{W}}_1} + {{\rm{W}}_2} = \left( {\dfrac{1}{2}mv_1^2 + mg{z_1}} \right) - \left( {\dfrac{1}{2}mv_2^2 + mg{z_2}} \right)\)
Do: \(\left\{ \begin{array}{l}{v_1} = 0\\{v_2} = 0\end{array} \right. \Rightarrow {{\rm{W}}_1} - {{\rm{W}}_2} = mg{z_1} - mg{z_2} = 0,02.10.\left( {5 - 3} \right) = 0,4J\)
Một vật có khối lượng \(2kg\) được đặt ở vị trí trong trọng trường và có thế năng tại đó \({{\rm{W}}_{{t_1}}} = 500J\). Thả vật rơi tự do đến mặt đất có thế năng \({{\rm{W}}_{{t_2}}} = - 900J\). Lấy \(g = 10m/{s^2}\). So với mặt đất vật đã rơi từ độ cao
Ta có:
+ Biến thiên thế năng chính bằng công của trọng lực: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = {A_P}\) (1)
+ \(\overrightarrow P \) hợp với phương rơi một góc \(\alpha = {0^0}\)
Ta suy ra công của trọng lực: \({A_P} = P.h = mgh\) (2)
Từ (1) và (2), ta suy ra: \({{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}} = mgh\)
\( \Rightarrow h = \dfrac{{{{\rm{W}}_{{t_1}}} - {{\rm{W}}_{{t_2}}}}}{{mg}} = \dfrac{{500 - \left( { - 900} \right)}}{{2.10}} = 70m\)
Vậy so với mặt đất, vật đã rơi từ độ cao \(h = 70m\)
Một vật rơi tự do từ độ cao 120m. Lấy g = 10m/s2. Bỏ qua sức cản của không khí. Động năng của vật gấp đôi thế năng tại độ cao
Chọn gốc thế năng tại mặt đất.
Cơ năng của vật tại vị trí vật bắt đầu rơi tự do:
\({{\rm{W}}_1} = {{\rm{W}}_{d1}} + {{\rm{W}}_{t1}} = \dfrac{1}{2}m.v_1^2 + mg.{z_1} = m.g.120 = 120.mg\,\,\left( J \right)\)
Cơ năng của vật tại vị trí có động năng gấp đôi thế năng là:
\(\left\{ \begin{array}{l}{{\rm{W}}_2} = {{\rm{W}}_{d2}} + {{\rm{W}}_{t2}}\\{{\rm{W}}_{d2}}{\rm{ = 2}}{{\rm{W}}_{t2}}\end{array} \right. \Rightarrow {{\rm{W}}_2} = {\rm{2}}{{\rm{W}}_{t2}} + {{\rm{W}}_{t2}} = 3{{\rm{W}}_{t2}}\)
Cơ năng được bảo toàn nên:
\(\begin{array}{l}{{\rm{W}}_1} = {{\rm{W}}_2} \Leftrightarrow 3{{\rm{W}}_{t2}} = {{\rm{W}}_1} \Leftrightarrow 3.mg.{z_2} = 120.mg\\ \Leftrightarrow {z_2} = \dfrac{{120}}{3} = 40\,\left( m \right)\end{array}\)
Có hai vật $m_1$ và $m_2$ cùng khối lượng $2m$, chuyển động thẳng đều cùng chiều, vận tốc $m_1$ so với $m_2$ có độ lớn bằng $v$, vận tốc của $m_2$ so với người quan sát đứng yên trên mặt đất cũng có độ lớn bằng $v$. Kết luận nào sau đây là sai?
Trong hệ quy chiếu gắn với quan sát, vật $m_1= 2 m$ có vận tốc bằng $2v$ nên động năng của vật là:
\({{\rm{W}}_d} = \dfrac{{{m_1}{{\left( {2v} \right)}^2}}}{2} = \dfrac{{8m{v^2}}}{2} = 4m{v^2}\)
=> Phương án C - sai
Một con lắc đơn có chiều dài 0,8 m. Kéo lệch dây treo con lắc hợp với phương thẳng đứng góc 600 rồi thả nhẹ. Bỏ qua lực cản không khí. Lấy g = 10 m/s2. Chọn gốc thế năng tại vị trí thấp nhất của vật. Tính tốc độ cực đại của con lắc đạt được trong quá trình dao động.
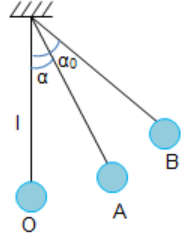
Chọn gốc thế năng tại O.
+ Cơ năng của vật tại O: \({{\rm{W}}_O} = {{\rm{W}}_{tO}} + {{\rm{W}}_{dO}} = \dfrac{1}{2}mv_{\max }^2\)
+ Cơ năng của vật tại B: \({{\rm{W}}_B} = {{\rm{W}}_{tB}} + {{\rm{W}}_{dB}} = mg.{z_B} = mg.l.\left( {1 - \cos {\alpha _0}} \right)\)
Áp dụng định luật bảo toàn cơ năng tại O và B ta có:
\(\begin{array}{l}{{\rm{W}}_O} = {{\rm{W}}_B} \Leftrightarrow \dfrac{1}{2}mv_{\max }^2 = mgl.\left( {1 - \cos {\alpha _0}} \right)\\ \Rightarrow {v_{\max }} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} = \sqrt {2.10.0,8.\left( {1 - \cos 60} \right)} = 2\sqrt 2 m/s\end{array}\)
Một viên đạn khối lượng $m= 100 g$ đang bay ngang với vận tốc $25 m/s$ thì xuyên vào một tấm ván mỏng dày $5 cm$ theo phương vuông góc với tấm vá. Ngay sau khi ra khỏi tấm ván vận tốc của viên đạn bằng $15 m/s$. Độ lớn của lực cản trung bình tấm ván tác dụng lên viên đạn bằng:
Do lực cản sinh công làm biến đổi động năng của vật nên áp dụng định lí biến thiên động năng:
\(\frac{{m{v_2}^2}}{2} - \frac{{m{v_1}^2}}{2} = - {F_c}s = > {F_c} = \frac{{-m\left( {{v_2}^2 - {v_1}^2} \right)}}{{2s}} = \frac{{ - 0,1\left( {{{15}^2} - {{25}^2}} \right)}}{{2.0,05}} = -400\,N\)
Một vật \(m = 1kg\) rơi từ O không vận tốc đầu ở độ cao \(120m\) xuống mặt đất. Chọn mốc thế năng tại mặt đất. Lấy \(g = 10m/{s^2}\).
a) Tính thế năng của vật tại vị trí thả vật.
b) Xác định độ cao mà tại đó vật có động năng bằng hai thế năng?
Chọn mốc thế năng tại mặt đất.
a) Tại vị trí thả vật có: \(\left\{ \begin{array}{l}v = 0\\m = 1kg\\g = 10m/{s^2}\\{h_0} = 120m\end{array} \right.\)
Thế năng của vật tại vị trí đó là:
\({W_t} = mgh = 1.10.120 = 1200J\)
b)
Cơ năng của vật tại vị trí thả vật:
\({W_0} = {W_{d0}} + {W_{t0}} = \frac{1}{2}m{v^2} + mg{h_0} = mg{h_0}\)
Cơ năng của vật tại vị trí động năng bằng hai lần thế năng \({W_d} = 2{W_t}\) là:
\(W = {W_t} + {W_d} = {W_t} + 2{W_d} = 3{W_t} = 3mg.h\)
Cơ năng được bảo toàn nên:
\(W' = W \Leftrightarrow 3mg.h = mg.{h_0}\)
\( \Rightarrow h = \dfrac{{{h_0}}}{3} = \dfrac{{120}}{3} = 40m\)
Trên mặt phẳng nhẵn nằm ngang, vật chịu tác dụng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) trong mặt phẳng và có phương vuông góc với nhau. Khi vật dịch chuyển được 5m từ trạng thái nghỉ, động năng của vật bằng bao nhiêu? Biết F1 = F2 = 10N
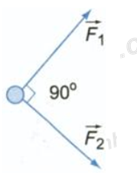
Hợp lực tác dụng lên vật:\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Do \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_2}} \) nên hợp lực có độ lớn là :
\(F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\)
Vật chuyển động theo hướng của lực \(\overrightarrow F \)nên công của hợp lực tác dụng lên vật là :
\({A_F}\; = F.s.\cos 0 = 10\sqrt 2 .5 = 50\sqrt 2 {\rm{ }}J\)
Vật dịch chuyển từ trạng thái nghỉ nên \({v_0}{\rm{ = 0}} \Rightarrow {{\rm{W}}_{d0}} = 0\)
Áp dụng định lí biến thiên động năng ta có:
\({A_F} = {{\rm{W}}_d} - {{\rm{W}}_{d0}} \Leftrightarrow {{\rm{W}}_d} = {A_F} = 50\sqrt 2 J\)

