Lực - tổng hợp và phân tích lực

Ta có: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha }$

$\begin{array}{*{20}{l}}{\alpha  = \left( {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right) \in \left[ {0;{{180}^0}} \right] \Rightarrow 1 \le \cos \alpha  \le 1}\\\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\cos \alpha  =  - 1 \Rightarrow {F_{\min }} = \left| {{F_1} - {F_2}} \right| \Leftrightarrow \overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_2}} }\\{\cos \alpha  = 1 \Rightarrow {F_{\max }} = {F_1} + {F_2} \Leftrightarrow \overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_2}} }\end{array}} \right.\\ \Rightarrow \left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\end{array}\end{array}$

Áp dụng vào bài ta có giá trị của hợp lực :

$\begin{array}{l}\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\\ \Leftrightarrow \left| {6 - 10} \right| \le F \le 6 + 10 \Leftrightarrow 4 \le F \le 16\end{array}$

Vậy giá trị của hợp lực không thể nhận giá trị 3N.

Ta có: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}$

Độ lớn của hợp lực: $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha }$

$\; \Rightarrow \left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2}$

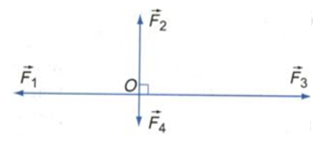
Hợp lực của bốn lực đồng quy là:

$\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}}$

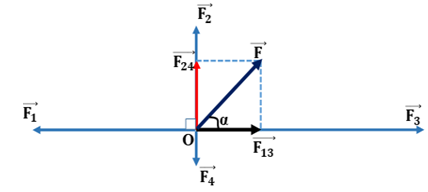
Vì $\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {{F_1}} \; \nearrow  \swarrow \;\overrightarrow {{F_3}} \;}\\{\overrightarrow {{F_2}}  \nearrow  \swarrow \;\overrightarrow {{F_4}} }\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{F_{13}} = {F_3} - {F_1}\; = 7 - 5 = 2N}\\{{F_{24}} = {F_2} - {F_4}\; = 3 - 1 = 2N}\end{array}} \right.$

Vì: $\overrightarrow {{F_{13}}}  \bot \;\overrightarrow {{F_{24}}}  \Rightarrow F = \sqrt {F_{13}^2 + F_{24}^2}  = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2 N$

Ta có: $\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha }$

$\begin{array}{*{20}{l}}{\alpha  = \left( {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right) \in \left[ {0;{{180}^0}} \right] \Rightarrow 1 \le \cos \alpha  \le 1}\\\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\cos \alpha  =  - 1 \Rightarrow {F_{\min }} = \left| {{F_1} - {F_2}} \right| \Leftrightarrow \overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_2}} }\\{\cos \alpha  = 1 \Rightarrow {F_{\max }} = {F_1} + {F_2} \Leftrightarrow \overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_2}} }\end{array}} \right.\\ \Rightarrow \left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\end{array}\end{array}$

Áp dụng vào bài ta có giá trị của hợp lực:

$\begin{array}{l}\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\\ \Leftrightarrow \left| {7 - 11} \right| \le F \le 7 + 11 \Leftrightarrow 4 \le F \le 18\end{array}$

Vậy giá trị của hợp lực không thể nhận giá trị $19N.$

Ta có: 

$\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{\vec F = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} }\\{\alpha  = \left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right) = {{120}^0}}\\{{F_1} = {F_2} = 30N}\end{array}} \right.\\ \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha }  = 45N\end{array}$

Ta có: Lực là đại lượng véc tơ đặc trưng cho tác dụng của vật này lên vật khác mà kết quả là gây ra gia tốc cho vật hoặc làm cho vật biến dạng.

A, C, D – đúng

B – sai vì: Lực có thể gây ra gia tốc cho vật hoặc làm cho vật biến dạng

A, B, D – sai vì còn phụ thuộc vào hướng của 2 lực thành phần

C - đúng

Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.

Các lực thay thế gọi là các lực thành phần

A - đúng

B – sai vì: Khi phân tích một lực thành hai lực thành phần thì phải tuân theo quy tắc hình bình hành

C – sai vì: Khi phân tích một lực thành hai lực thành phần thì hai lực thành phần làm thành hai cạnh của hình bình hành.

D – sai

Điều kiện của hợp lực: $\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}$

A, B, C – sai

D - đúng

Hợp lực của hai lực đồng quy hợp với nhau một góc $\alpha$: ${F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}cos\alpha$

Ta có: $\left\{ \begin{array}{l}\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \\F = {F_1} + {F_2}\end{array} \right. \Rightarrow \overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_2}}$ hay $\alpha  = {0^0}$

Ta có: $\left\{ \begin{array}{l}\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \\F = {F_1} - {F_2}\end{array} \right. \Rightarrow \overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_2}}$ hay $\alpha  = {180^0}$

Ta có, hợp lực F
$\begin{array}{l}\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\\ \Leftrightarrow 12 - 9 \le F \le 12 + 9\\ \Leftrightarrow 3N \le F \le 21N\end{array}$

$\Rightarrow F = 15N$ có thể là độ lớn của hợp lực.

Ta có, hợp lực của hai lực thành phần $F = \sqrt {{F_1}^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\alpha }$

=> F phụ thuộc vào:

+ Độ lớn của hai lực ${\overrightarrow F _1}$ và ${\overrightarrow F _2}$

+ Góc giữa hai lực ${\overrightarrow F _1}$ và ${\overrightarrow F _2}$

Ta có: Hợp của tất cả các lực tác lên vật gọi là cân bằng khi các lực tác dụng lên nó bằng $\overrightarrow 0$

$\overrightarrow F  = {\overrightarrow F _1} + {\overrightarrow F _2} + ... + {\overrightarrow F _n} = \overrightarrow 0$

A, B, C – là trạng thái cân bằng của chất điểm

D – không là trạng thái cân bằng của chất điểm do có lực tác dụng lên vật khác không.

Ta có: Hai lực được gọi là cân bằng khi chúng có cùng phương, ngược chiều và cùng độ lớn

$\Rightarrow$ Chất điểm ấy cân bằng khi hai lực ngược hướng (cùng phương, ngược chiều) và có cùng độ lớn.

Ta có, hợp lực của hai lực thành phần $F = \sqrt {{F_1}^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\alpha }$

Thay số vào, ta được:

$\begin{array}{l}F = \sqrt {{F_1}^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\alpha } \\ = \sqrt {{{30}^2} + {{30}^2} + 2.30.30{\rm{cos12}}{{\rm{0}}^0}} \\ = 30N\end{array}$

Ta có, ba lực 12N, 10N, 16N khi tác dụng vào vật mà vật đứng cân bằng thì hợp lực của chúng bằng 0

=> Khi tác dụng bỏ lực 10N vào vật thì hợp lực của 2 lực còn lại đó có độ lớn chính bằng 10N

Ta có, điều kiện của hợp lực: $\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}$

Phương án A : $0 \le F \le 19N$

Phương án B: $6N \le F \le 26N$

Phương án C: $30N \le F \le 62N$

Phương án D: $34N \le F \le 66N$

=> Lực có môđun $20N$ là hợp lực của hai lực thành phần $16N$ và $10N$

Ta có: $\overrightarrow {{F_1}}  \bot \overrightarrow {{F_2}}$

$\begin{array}{l} \Rightarrow {F^2} = F_1^2 + F_2^2\\ \Rightarrow {F_2} = \sqrt {{F^2} - F_1^2}  = \sqrt {{{100}^2} - {{60}^2}}  = 80N\end{array}$