Câu hỏi:
2 năm trước
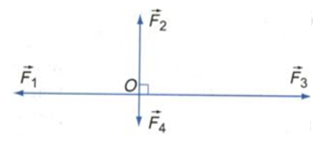
Tìm hợp lực của bốn lực đồng quy trong hình vẽ. Biết \({F_1}\; = 5N,{F_2}\; = 3N,{F_3}\; = 7N,{F_4}\; = 1N\)
Trả lời bởi giáo viên
Đáp án đúng: a
Hợp lực của bốn lực đồng quy là:
\(\vec F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{24}}} \)
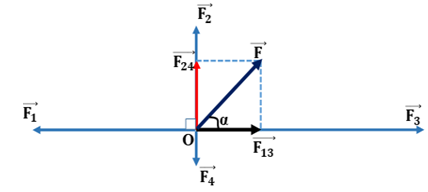
Vì \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {{F_1}} \; \nearrow \swarrow \;\overrightarrow {{F_3}} \;}\\{\overrightarrow {{F_2}} \nearrow \swarrow \;\overrightarrow {{F_4}} }\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{F_{13}} = {F_3} - {F_1}\; = 7 - 5 = 2N}\\{{F_{24}} = {F_2} - {F_4}\; = 3 - 1 = 2N}\end{array}} \right.\)
Vì: \(\overrightarrow {{F_{13}}} \bot \;\overrightarrow {{F_{24}}} \Rightarrow F = \sqrt {F_{13}^2 + F_{24}^2} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 N\)
Hướng dẫn giải:
Sử dụng quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng.
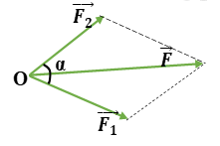
Biểu thức: \(\vec F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \)
