Chuyển động tròn đều

Tốc độ góc của kim phút và kim giờ: 

$\left\{ \matrix{ {\omega _{phut}} = {\pi \over {1800}}rad/s = {\omega _1} \hfill \cr {\omega _{gio}} = {{2\pi } \over {43200}} = {\pi \over {21600}}rad/s = {\omega _2} \hfill \cr} \right.$

Gọi ∆t là thời gian ngắn nhất từ lúc 15h đến khi hai kim trùng nhau.

Góc kim giờ quét trong ∆t là: $\alpha  = {\omega _{gio}}\Delta t = {\pi  \over {21600}}.\Delta t\,\,\,\left( {rad} \right)$

Góc kim phút quét trong ∆t là: $\beta  = {\omega _{phut}}\Delta t = {\pi  \over {1800}}.\Delta t\,\,\,\left( {rad} \right)$

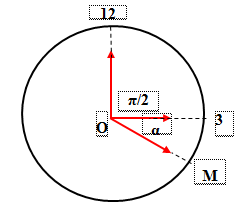
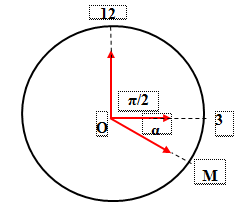
Từ hình vẽ ta có :

$\beta  - \alpha  = {\pi  \over 2} \Rightarrow {{\pi .\Delta t} \over {1800}} - {{\pi .\Delta t} \over {21600}} = {\pi  \over 2} \Rightarrow \Delta t = 981,82s \approx 16,36phut$

Vệ tinh chuyển động tròn đều với bán kính $r = R + h = 6400 + 400 = 6800km$, có tâm trùng với tâm Trái Đất.

Ta có tốc độ dài v = 7,820km/s

Tốc độ góc : $\omega  = \dfrac{v}{r} = \dfrac{{7,82}}{{6800}} = 1,{15.10^{ - 3}}rad/s$

Chu kì: $T = \dfrac{{2\pi }}{\omega } \approx 5461s$

Cách giải:

Tần số: f = 5 vòng/phút $= \frac{1}{{12}}$ vòng/s

Tốc độ góc của chuyển động tròn đều là: $\omega  = 2\pi .f = 2\pi .\frac{1}{{12}} = \frac{\pi }{6}\,rad/s$

Gia tốc hướng tâm của em bé đó là: ${a_{ht}} = {\omega ^2}r = {\left( {\frac{\pi }{6}} \right)^2}.3 \approx 0,82m/{s^2}$

+ Chất điểm quay hết 20 vòng mất 4s

$\Rightarrow$ Chất điểm quay 1 vòng mất $\dfrac{4}{{20}} = 0,2s$

$\Rightarrow T = 0,2s$

+ Tốc độ dài: $v = \omega r = \dfrac{{2\pi }}{T}.r = \dfrac{{2\pi }}{{0,2}}.0,5 = 5\pi \,\left( {m/s} \right)$

Ta có: $\left\{ \begin{array}{l}a = {\omega ^2}R\\\omega  = \dfrac{{2\pi }}{T}\end{array} \right. \Rightarrow a = {\left( {\dfrac{{2\pi }}{T}} \right)^2}.R$

Ta có: ${a_{ht}} = \dfrac{{{v^2}}}{r} \Rightarrow {a_{ht}} \sim {v^2}$

$\Rightarrow$ v tăng 2 lần thì gia tốc hướng tâm tăng 4 lần.

Bán kính của bánh xe: $r = 25cm = 0,25m$

Tốc độ của ô tô: $v = 36km/h = 10m/s$

Gia tốc hướng tâm: ${a_{ht}} = \dfrac{{{v^2}}}{r} = \dfrac{{{{10}^2}}}{{0,25}} = 400m/{s^2}$

Chu kì: $T = 90{\rm{ }}phu t = 5400s$

Có: $r = 6380 + 320 = 6700km = 6\,700{\rm{ }}000m$

Vận tốc:  $v = \omega r = \dfrac{{2\pi }}{T}.r = \dfrac{{2.3,14}}{{5400}}.6700000 \approx 7792m/s$

Gia tốc hướng tâm: ${a_{ht}} = \dfrac{{{v^2}}}{r} = \dfrac{{{{7792}^2}}}{{6700000}} \approx 9,062m/{s^2}$

Ta có: $\left\{ \begin{array}{l}{T_h} = 12h\\{T_p} = 1h\\{R_h} = 30cm\\{R_p} = 40cm\end{array} \right.$

Lại có: $\left\{ \begin{array}{l}{v_p} = \dfrac{{2\pi }}{{{T_p}}}.{R_p}\\{v_h} = \dfrac{{2\pi }}{{{T_h}}}.{R_h}\end{array} \right. \Rightarrow \dfrac{{{v_p}}}{{{v_h}}} = \dfrac{{{T_h}.{R_p}}}{{{T_p}.{R_h}}} = \dfrac{{12.40}}{{1.30}} = 16$

Ta có: $\left\{ \begin{array}{l}{a_{ht}} = {\omega ^2}r\\{a_{ht}}' = {\left( {3\omega } \right)^2}.\dfrac{r}{3} = 3.{\omega ^2}r\end{array} \right. \Rightarrow {a_{ht}}' = 3.{a_{ht}}$

Tần số: $f = 5vong/phut = \dfrac{1}{{12}}vong/s$

Tốc độ góc của chuyển động tròn đều là:

$\omega  = 2\pi .f = 2\pi .\dfrac{1}{{12}} = \dfrac{\pi }{6}rad/s$

Gia tốc hướng tâm của em bé đó là:

${a_{ht}} = {\omega ^2}r = {\left( {\dfrac{\pi }{6}} \right)^2}.3 \approx 0,82m/{s^2}$

Chuyển động tròn là chuyển động có quỹ đạo là một đường tròn

Chuyển động tròn đều là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.

Ta có:

Chuyển động tròn đều là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.

=> Chuyển động quay của kim phút trên mặt đồng hồ chạy đúng giờ là chuyển động tròn đều

A - sai vì: véctơ vận tốc của chuyển động tròn đều luôn thay đổi

B - đúng

C, D sai vì: tốc độ góc $\omega  = \dfrac{{\Delta \varphi }}{t} = \dfrac{v}{r}$ và gia tốc ${a_{ht}} = \dfrac{{{v^2}}}{r}$ đều phụ thuộc vào bán kính quỹ đạo.

A, B, D - đúng

C - sai vì: ${a_{ht}} = \dfrac{{{v^2}}}{r} = {\omega ^2}r$

A - sai véctơ vận tốc có hướng luôn thay đổi và gia tốc khác 0

B - sai vì độ lớn của gia tốc tỉ lệ nghịch với bán kính quỹ đạo: ${a_{ht}} = \dfrac{{{v^2}}}{r} = {\omega ^2}r$

C - sai vì độ lớn của vận tốc không đổi

D - đúng

Chu kì T của chuyển động tròn đều là khoảng thời gian để vật đi được một vòng.

$T = \frac{{2\pi }}{\omega }$

Đơn vị: Giây (s)

A - sai vì tần số là số vòng mà vật đi được trong $1$ giây

B - sai vì $f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}$

C - sai vì đơn vị của tần số là Hz hay s^-1

D - đúng

A, B, D - đúng

C - sai vì: mối liên hệ giữa tốc độ dài và tốc độ góc: $v = \omega r$ hay $\omega  = \frac{v}{r}$